多角形から角を求める Youtube
まずbの角度から求めていきます。向かい合った角、つまり対頂角は等しいので、b=30° 次にaの角度を求めます。直線の角の大きさは180°です。そのためaの角度は、180°30°=150° cの角度は対頂角よりaと等しいので、c=150° よって、 答え a=150°、b=30°、c 公式をつかわない!扇形の中心角の求め方3つのステップ それじゃあ、なぜこの公式で扇形の中心角が求められるのか?? ちょっと気になるよね?? じつは、扇形の中心角の公式は、 比例式をつかった中心角の求め方 から導きだしたものなんだ。
多 角形 の 角度 の 求め 方
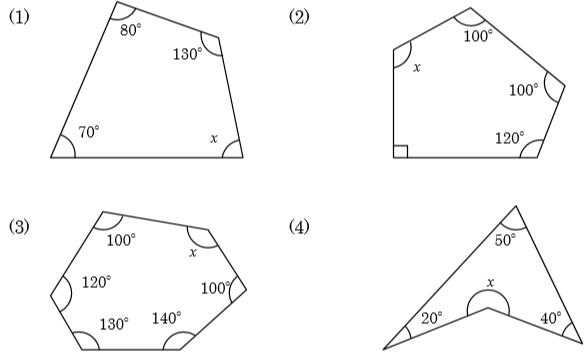
多 角形 の 角度 の 求め 方-通常の多角形は2次元の凸状の形をしていて、長さの等しい辺と角度の等しい角で構成されています。 四辺形や三角形 は簡単な公式で面積を求めることができるものの、辺の数が5つ以上の多角形の面積を求めるのであれば、その形状の辺心距離と外周をを用いた方が良いでしょう。 わずかな内角の和の公式から 正十五角形だと分かるので1つの外角は 図の の大きさを求めなさい。 補助(延長)線を引いて内角の和などを利用して求まります。 こういう形をした多角形を凹多角形といいますが、気にしなくて良いです。 笑 四角形や三角形に
正六角形 正6角形 の角度の求め方は 1分でわかる値 内角の和 外角 正多角形の角度の求め方
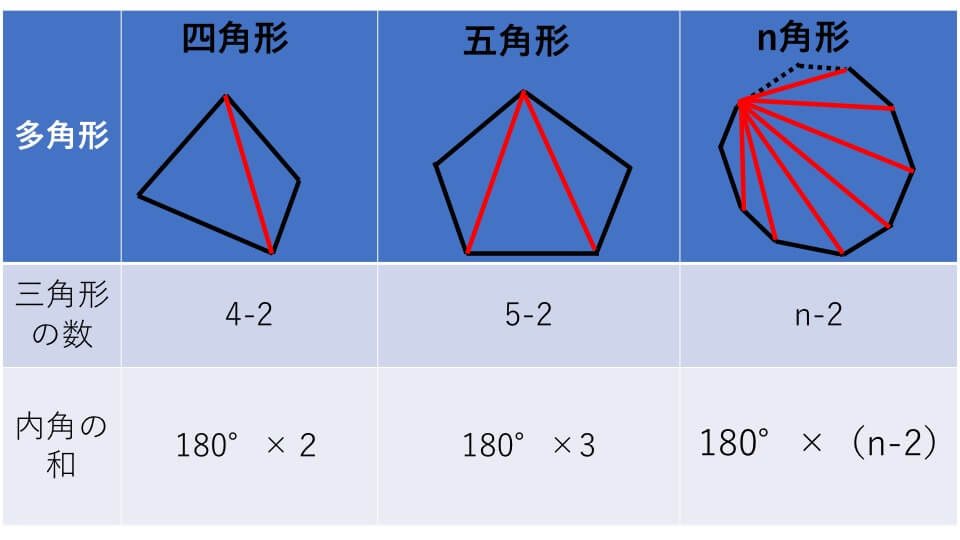
直角三角形の底辺と角度から、高さ・斜辺・面積を計算します。 底辺と角度を入力し「高さ・斜辺・面積を計算」ボタンをクリックすると、入力された直角三角形の高さと斜辺と面積が表示されます。 底辺a: 角度θ: 度 ラジアンこれが上で求めた表の値と合致します。 これを他の角に対しても用いることが出来るように式で表すと、 n角形の内角の和=180°×(n2) となります。これで、いくら角が大きな多角形であっても、その内角の和を知ることが出来ます! 外角の和の求め方を考えるN角形の内角の和=180×(n-2) この公式を忘れてしまったらどうしたらよいでしょうか? 多角形の内角の和は求められないでしょうか? そんなことはありません。 忘れてしまった場合は、前項で使用したこんな表を自分で作成してみましょう。 三角形
この公式考えた人にでも聞くしかないかと-w- 『このような計算式をつかい、こう計算すれば多角形の内角の和が求められる』っていう風に覚えるしかないので、深く考えないほうがいいですよ。 ちなみに三角形は 180度×(3-2)=180度。 四角形は 180星形の内角の和が180°になる理由 星形の角度が180°になる理由を説明していくために 三角形の外角の性質を知っておく必要があります。 このように 三角形の外角は、隣にない内角2つ分を合わせた大きさになるという性質があります。 これを利用してこの記事では、三角関数の角度の求め方や変換公式( など)についてわかりやすく解説していきます。 三角方程式・三角不等式の計算問題もていねいに説明していくので、この記事を通してぜひマスターしてくださいね! 目次 非表示 三角関数の角度の
多 角形 の 角度 の 求め 方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
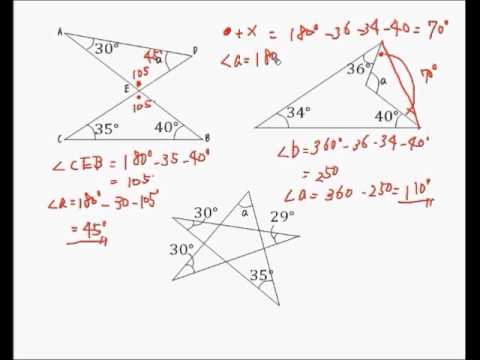
 中2数学 複雑な多角形 角の和 応用問題 | 中2数学 複雑な多角形 角の和 応用問題 | 中2数学 複雑な多角形 角の和 応用問題 |
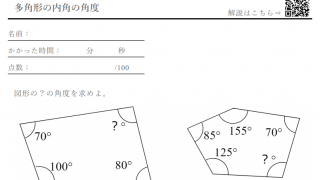
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
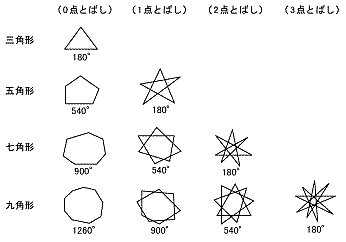
中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
「多 角形 の 角度 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 中2数学 複雑な多角形 角の和 応用問題 | 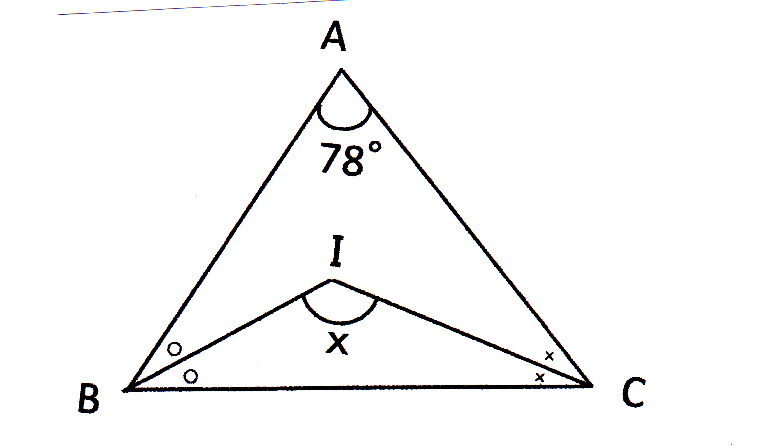 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
「多 角形 の 角度 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 | 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 | 中2数学 複雑な多角形 角の和 応用問題 |
「多 角形 の 角度 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 | 中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 | 中2数学 複雑な多角形 角の和 応用問題 |
「多 角形 の 角度 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
中2数学 複雑な多角形 角の和 応用問題 | 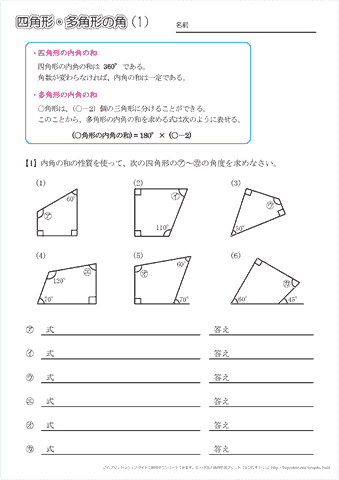 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
「多 角形 の 角度 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 中2数学 複雑な多角形 角の和 応用問題 | 中2数学 複雑な多角形 角の和 応用問題 | 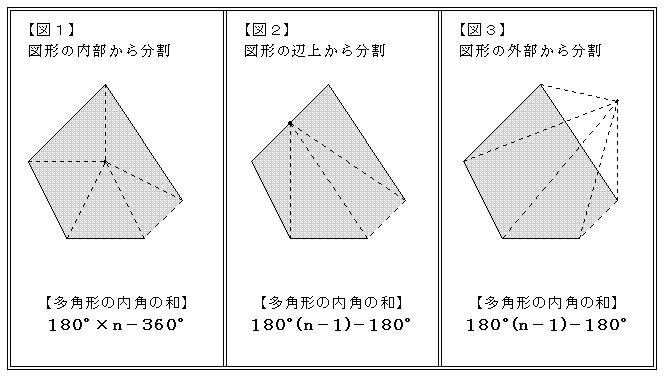 中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
「多 角形 の 角度 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 中2数学 複雑な多角形 角の和 応用問題 | 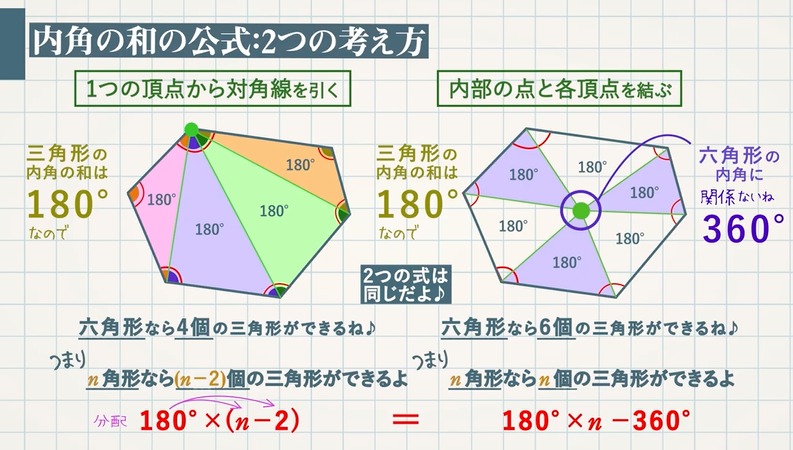 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 | 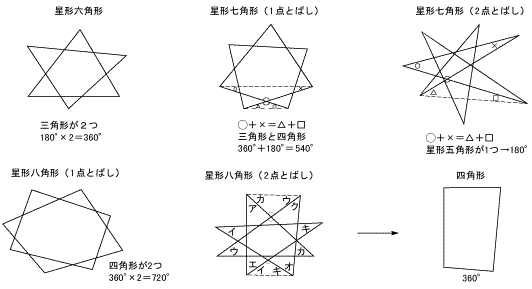 中2数学 複雑な多角形 角の和 応用問題 | 中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 | 中2数学 複雑な多角形 角の和 応用問題 |
「多 角形 の 角度 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 | 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
「多 角形 の 角度 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 中2数学 複雑な多角形 角の和 応用問題 | 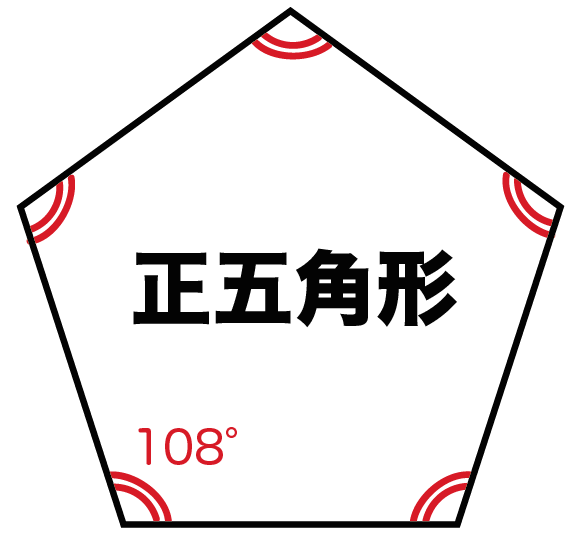 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 | 中2数学 複雑な多角形 角の和 応用問題 |
「多 角形 の 角度 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 中2数学 複雑な多角形 角の和 応用問題 | 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
「多 角形 の 角度 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 |
 中2数学 複雑な多角形 角の和 応用問題 |  中2数学 複雑な多角形 角の和 応用問題 | 中2数学 複雑な多角形 角の和 応用問題 |
中2数学 複雑な多角形 角の和 応用問題 |
すると、以下のように度数表記の角度が求められるのです。 このようにして、三角形において斜辺と底辺か挟まれた角度を計算することができるのです。 さまざまなパターンの三角形の角度の計算に慣れ、すぐに対応できるようにしておきましょう。 関連A → = ( a 1, a 2, a 3) と b → = ( b 1, b 2, b 3) のなす角 θ を計算してくれるツールです。 平面ベクトルの場合は、 a 3 = b 3 = 0 としてください。 ※あくまで計算の確認程度にお使いください。 次回は 等差数列の一般項の求め方の証明と例題 を解説します。





0 件のコメント:
コメントを投稿