[最新] parabola y=4x-x^2 280074

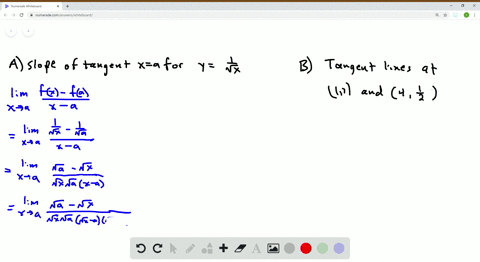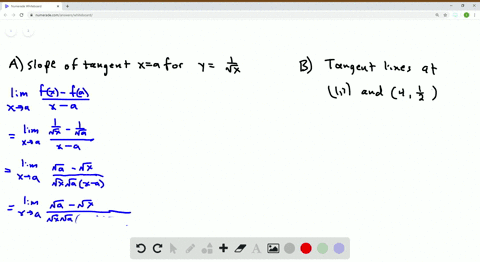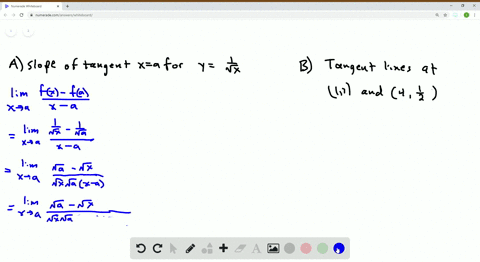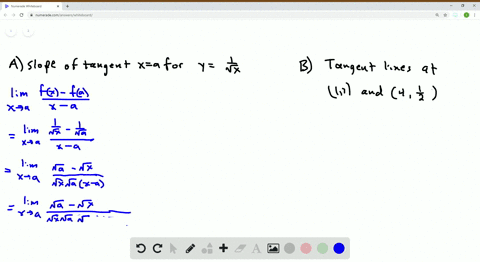
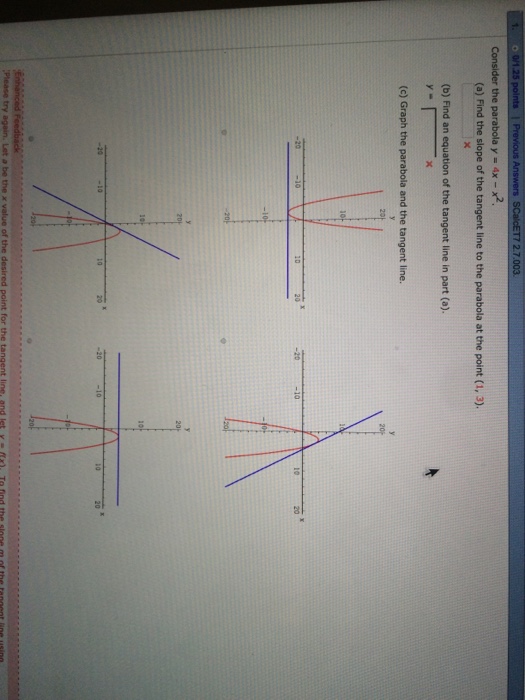
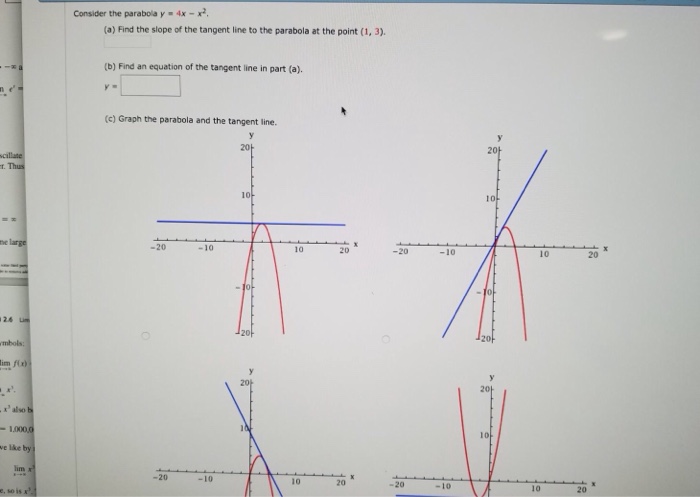
Click here👆to get an answer to your question ️ The circle x^2 y^2 2lambda x = 0, lambda∈ R touches the parabola y^2 = 4x externally, thenA parabola is the set of all points ( x, y) \displaystyle \left (x,y\right) (x, y) in a plane that are the same distance from a fixed line, called the directrix, and a fixed point (the focus) not on the directrix We previously learned about a parabola's vertex and axis of symmetry 1 Find the slope of the line tangent to the parabola y = 4x – x ^ 2 At point (1,3) a) Using the definition of the limit first and then using derivation rules (derived from polynomials) b) Find the equation of the tangent line at the point (1,3) c) find the approximate value of "y" when x = 11;

The Area Bounded By The Curve Y 4x X 2 And X Axis Is A 30 7 Sq Units B 31 7 Sq Units Youtube

Parabola y=4x-x^2

Parabola y=4x-x^2- Given Two curves are y 2 = 4x and y = 2x – 4 Now to find the area between these two curves, we have to find common area ie Shaded portion Intersection of parabola y 2 = 4x with line y = 2x – 4 Putting the value of y from the equation of a line in parabola equation, we get,MCQ Parabola 1 The equation of the tangent at the vertex of the parabola x 2 4x 2y = 0 is (D) y = –2 2 BC is latus rectum of a parabola y 2 = 4ax and A is its vertex, then minimum length of projection of BC on a tangent drawn in portion BAC is 3 The coordinates of the point on the parabola y = x 2 7x 2 , which is nearest to

The Point Of Intersection Of The Tangents To The Parabola Y 2 4x At The Points Where The Circle X 3 2 Y 2 9 Meets The Parabola Other Than The Origin Is

Hence, The equation of the directrix of the parabola y 2 4x 4y 2 = 0 is \(x=\dfrac{3}{2}\) Download Solution PDF Share on Whatsapp India's #1 Learning Platform Start Complete Exam Preparation Daily Live MasterClasses Practice Question Bank Mock Tests & Quizzes Get Started for Free Download AppParabola 09 The equation of circle touching the parabola at upper end of its latus rectum and passing through its vertex, is y=0 (A)2x2 2y2 x2y=0 2x2 2y2 x – 3y = 0 9 (B) 2x2 2y2 4x 2 (D) 2x2 2y2 – 7xy=0The class is working with Quadratic functions and graphs – I'm supposed to find the vertex and intercepts , then sketch its graph l really need help y= x^2 4x 12 This is a headscratcher for me Thanks for all of the help It is appreciated Answer by Alwayscheerful(414) (Show Source)Parabola, Finding the Vertex 31 Find the Vertex of y = x 24x12 Parabolas have a highest or a lowest point

Points 2 years ago Dear student focus of y^2 = 4x is (1,0) focal chord inclined at an angle of 45 degree from x axis y – 0 = 1 (x 1) y = x – 1 Hope it helps RegardsGraph y=4xx^2 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Reorder and The directrix of a parabola is the horizontal line found by subtracting from the ycoordinate of the vertex if the parabolaThe equation of the line through the point (0,1,2) and perpendicular to the line The equation of the line whose slope is 3 and which cuts off an intercept 3 from the positive xaxis is The Equation Of The Normal Line To The Curve Y X Loge X Parallel To 2x 2y 3 0 Is The Equation Of The Normal To The Curve Y 4 Ax Cube At A A Is

Find the area of the region bounded by the parabola y^2 = 4x, the xaxis, and the lines x = 1 and x = 4 asked in Definite Integrals by Siwani01 ( 504k points) area of bounded regionsGraph a parabola by finding the vertex and using the line of symmetry and the yinterceptDetermine if x 2 4x8y12=0 is the equation of a parabola If so, find the coordinates of the vertex and the focus and the equation of the directrix Since only the x terms are quadratic, we only need complete the square on these terms

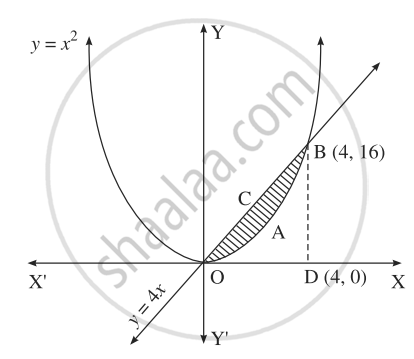
Find The Area Of The Region Included Between Y X2 And The Line Y 4x Mathematics And Statistics Shaalaa Com

Solved Consider The Parabola Y 4x X2 A Find The Slope Chegg Com

Watch Video in App Continue on Whatsapp This browser does not support the video elementGraph y^2=4x y2 = 4x y 2 = 4 x Rewrite the equation as 4x = y2 4 x = y 2 4x = y2 4 x = y 2 Divide each term by 4 4 and simplify Tap for more steps Divide each term in 4 x = y 2 4 x = y 2 by 4 4 4 x 4 = y 2 4 4 x 4 = y 2 4 Cancel the common factor of 4 4The equation of the common tangent touching the circle (x 3)^2 y^2 = 9 and the parabola y^2 = 4x above the xaxis is

Find The Area Of The Region Bounded By The Parabola Y 2 4x The X Axis And The Lines X 1 And X 4 Sarthaks Econnect Largest Online Education Community

Find The Area Lying Above The X Axis And Under The Parabola Y 4x X2 Maths Meritnation Com

 Given the Equation #color(red)(y=f(x)=4x^2# A Quadratic Equation takes the form #color(blue)(y=ax^2bxc# Graph of a quadratic function forms a Parabola The coefficient of the #color(red)(x^2# term (a) makes the parabola wider or narrow If the coefficient of the #color(red)(x^2,# term (a) is negative then the parabola opens down The term Vertex is usedSo we're asked to find the slope of the tangent line at a problem Considering the equation of the problem is four x minus x squared And this this tangent line is going to be at the 01 comma three So first of all we're asked to find the slope of this tangent line Well the slope is the derivative dy over dx which is Taking the derivative that that's 4 2 x mm La inconsistencia viene de suponer que texy^ {2} 4x = 0 /tex es una parábola tomando x como variable independiente Ya lo resolví, hay que despejar la ecuación de forma que sea valida para la parábola y^24x=0 a y^2=4x se despeja con la formula y^2=4P por tanto 4P=4 > p=4/4 > P=1 como P=1 el foco vale (1,0) asi que la parabola

Solution There Are Two Tangent Line To The Curve Y 4x X 2 That Pass Through The Point 2 5 Find The Equations Of These Two Lines And Make A Sketch To Verify Your Results

Graph The Parabola Y X 2 4x 1 Youtube

 The original question from Anuja asked how to draw y 2 = x − 4 In this case, we don't have a simple y with an x 2 term like all of the above examples Now we have a situation where the parabola is rotated Let's go through the steps, starting with a basic rotated parabola Example 6 y 2 = x The curve y 2 = x represents a parabola rotatedThe Parabola Given a quadratic function f ( x) = a x 2 b x c, it is described by its curve y = a x 2 b x c This type of curve is known as a parabola A typical parabola is shown here Parabola, with equation y = x 2 − 4 x 5 benjaminec / Getty Images Finding the yintercept of a parabola can be tricky Although the yintercept is hidden, it does exist Use the equation of the function to find the yintercept y = 12x 2 48x 49 The yintercept has two parts the xvalue and the yvalue

Solved A Find The Slope Of The Tangent Line To The Parabola Y 4x X 2 At The Point 1 3 I Using Definition 1 Ii Using Equation 2 B Find An

What Is The Area Bounded By X Axis And The Curve Math Y 4x X 2 Math Quora

Answer (1 of 5) Well, the cavity is the same, just concave down The vertex is (2,10) Remember, X coordinate of a vertex is b/2a, as it's the average of and in Find the area of the region bounded by the parabola y = 3x^2, the tangent line to this parabola at (1, 3), and the xaxis Calculus Find the parametric equations for the line of intersection of the planes xyz=3 and xy2z=2 I took the cross product of the 2 equations and got 3ij2k I then set z=0 and got x=5/2 and y=1/2 Find the area of the region bounded by the parabola y = 4x^2, the tangent line to this parabola at (4, 64), and the xaxis CALCULUS The region R is bounded by the xaxis, yaxis, x = 3 and y = 1/(sqrt(x1)) A Find the area of region R B Find the volume of the solid formed when the region R is revolved about the xaxis C

Example 7 Find Area Lying Above X Axis Included B W Circle

The Area Bounded By The Curve Y 4x X2 And The X Axis Is A 307sq Units Maths 1745 Meritnation Com

 For the parabola in the xyplane, find the following y =x^2 −4x−12 (a) The xintercepts (b) The yintercept (c) Coordinates of the vertex a and x=−2 x=6 b y=−12 c 2,−16 Math Review Question 19 Page 245 Difficulty mediumA tangent to a parabola is a straight line which intersects (touches) the parabola exactly at one point at x = 2 with slope 3 Let (x, y) be the point where we draw the tangent line on the curve Slope of the required tangent (x, y) is 3 Equation of the tangent line is 3xy2 = 0 at which the tangent is parallel to the x axisFree Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience

Solved Consider The Parabola Y 4x X2 A Find The Slope M Of The Tangent Line To The Parabola At The Point 1 3 I Using This Denition The Course Hero

The Area Bounded By The Curve Y 4x X 2 And X Axis Is A 30 7 Sq Units B 31 7 Sq Units Youtube

To update y = 3(x 2 4x 4) 1 12 We have now successfully completed the square Now we need to get this into more friendly terms The inside of the parenthesis (the completed square) can be simplified to (x 2) 2 The final version after the smoke clears is y = 3(x 2) 2 11Find the equation of common tangent to the parabola y 2 = 4x and x 2 = 32y Advertisement Remove all ads Solution Show Solution Given equation of the parabola is y 2 = 4x Comparing this equation with y 2 = 4ax, we get 4a = 4 ∴ a = 1 Let the equation of common tangent be y=4x^{2 4x9 Find the xintercepts for the parabola Register Now Username * EMail * Password * Confirm Password * Answer The parabola does not intercept the xaxis Stepbystep explanation The parabola intercepts the xaxis when ,

Find The Area Enclosed By The Parabolas Y 4x X 2 And Y X 2 X Sarthaks Econnect Largest Online Education Community

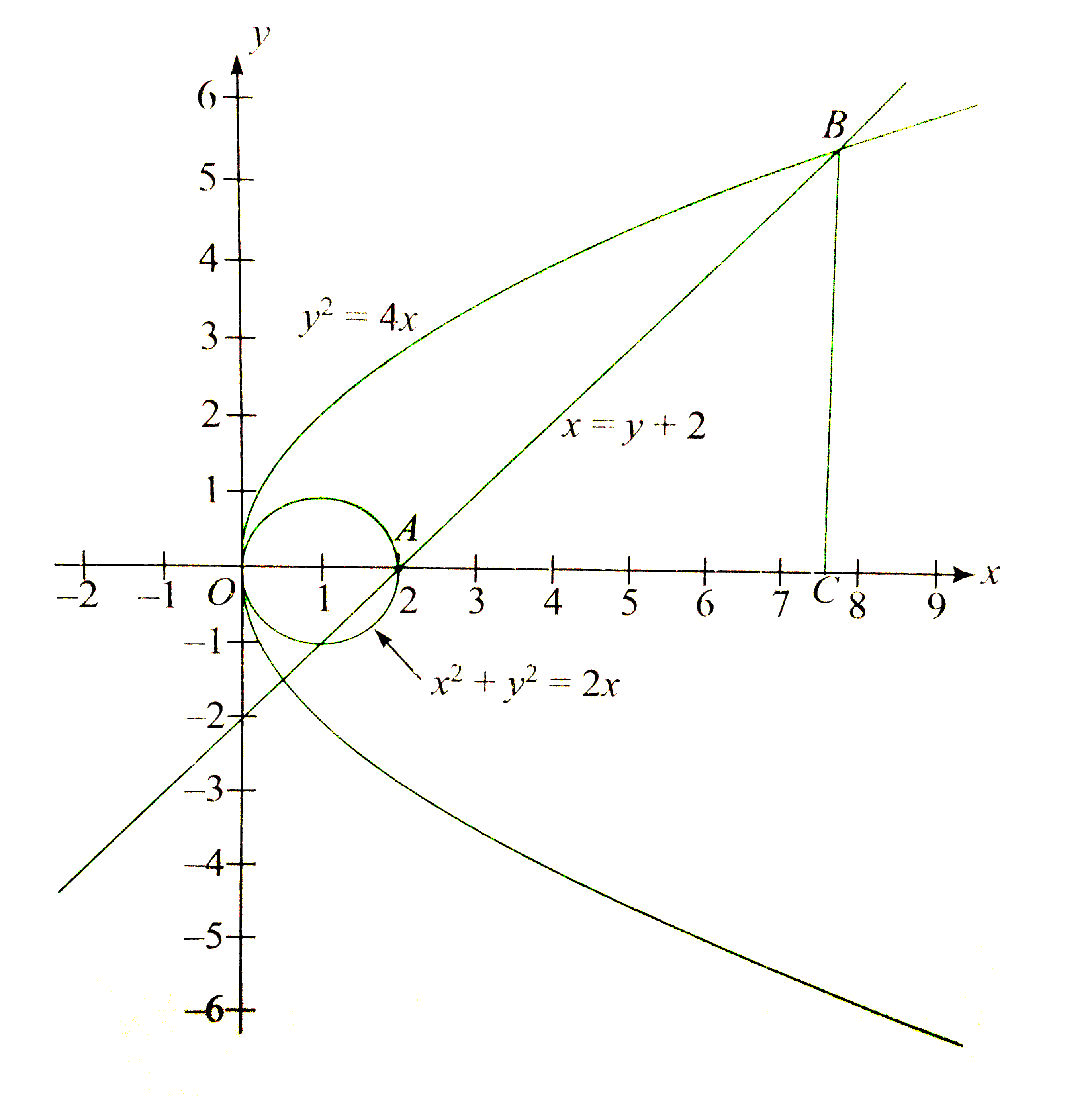
Find The Area Bounded By Y 2lt 4x X 2 Y 2geq2x A N Dxlt Y 2 In The First Quadrant

 Get answer The parabola `y^2 = 4x` and the circle `x^2 y^2 6x 1=0` NWDA various post vacancy 21 for 62 posts, apply before 25 June 21 Check steps to apply, eligibility, vacancy, salary, selection process & education qualification (y')² = 4x' Según el punto dado P₁(2,3), verificamos si este punto pertenece a la parábola (3)² = 4x' → x' = 9/4 ≠ 2 Podemos observar que el punto no pertenece a la parábola, por tanto el vértice se encuentra con vértice en el origen O' Adjunto podemos observar la gráficaAssuming you don't know

Misc 15 Find Area X Y Y2 4x 4x2 4y2 9 Miscellaneous

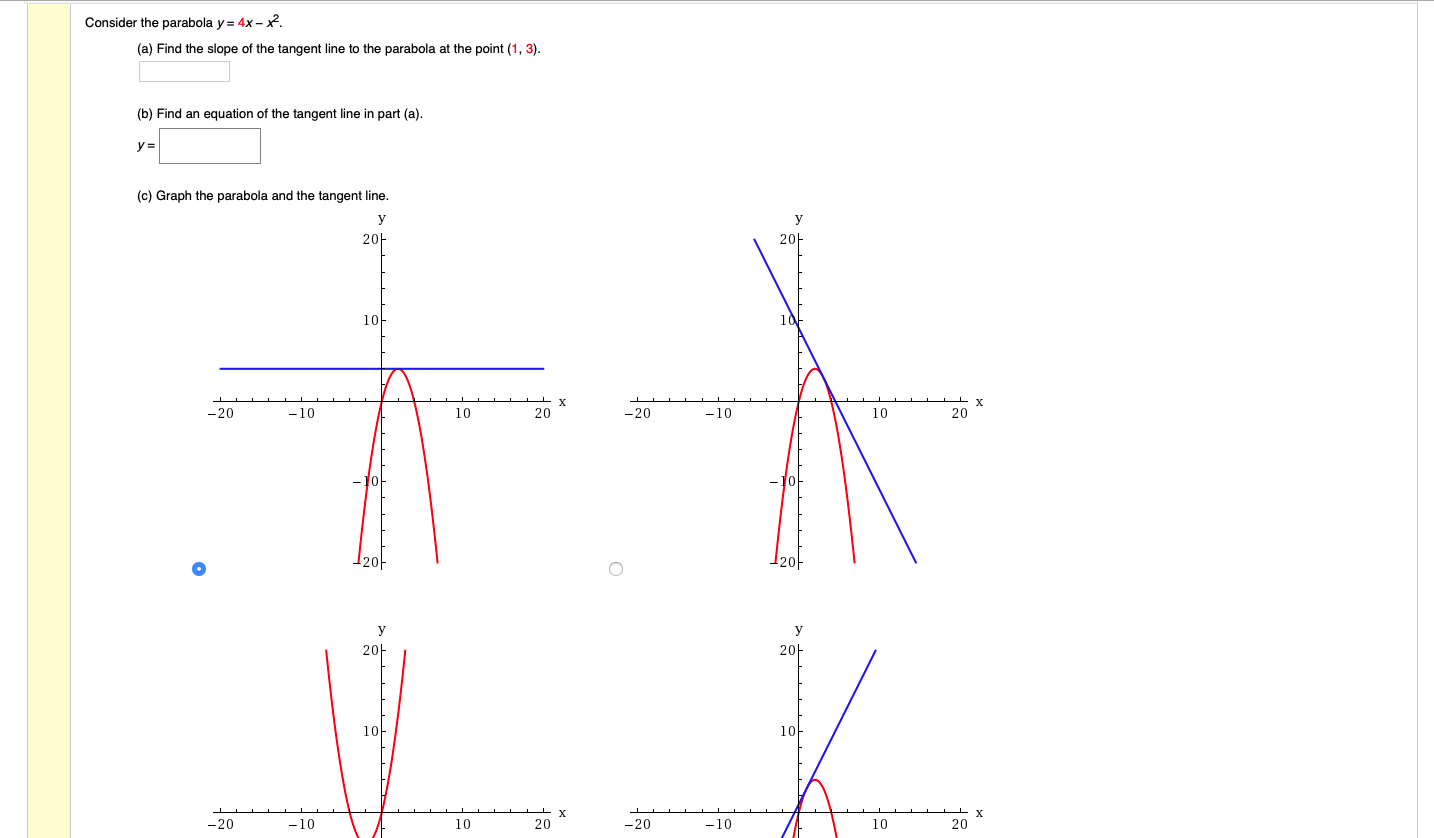
Solved Consider The Parabola Y 4x X2 A Find The Slope Chegg Com

In the image you can see that the outer radius is $2$, not $1$ and the inner radius is $1x^2$ Furthermore, you were subtracting in the wrong orderSo we're asked to find the slope of the tangent line at a problem Considering the equation of the problem is four x minus x squared And this this tangent line is going to be at the 01 comma three So first of all we're asked to find the slope of this tangent line Well the slope is the derivative dy over dx which is Taking the derivative that that's 4 2 x mmStack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange

What Is The Volume Of The Solid Bounded By The Parabola Y 4x 2 And The Lines X 0 And Y 16 By Revolving About The Line Y 2 Quora

The Area Bounded By The Curves Y 2 4x And X 2 4y Youtube

 When we have the equation of a parabola, in the form y = ax^2 bx c, we can always find the x coordinate of the vertex by using the formula x = b/2a So we just plug in the values In this case, the equation in form y = ax^2 bx c is equal to y=x^2 4x 12Click here👆to get an answer to your question ️ If two different tangents of y^2 = 4x are the normals to x^2 = 4by then The area of the triangle formed by the tangent and the normal to the parabola y 2 = 4 a x, both drawn at the same end of the latus rectum, and the axis of the parabola is Hard Find the area bounded by the parabola `y^2=4x` and the straight line `xy=3` Updated On To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now!

The Region Between Y 4x X 2 And The X Axis Is Rotated Around The Y 6 Line How Can I Find The Volume Of The Object Formed Quora

What Is The Area Bounded By X Axis And The Curve Math Y 4x X 2 Math Quora

Parabola Calculator This calculator will find either the equation of the parabola from the given parameters or the axis of symmetry, eccentricity, latus rectum, length of the latus rectum, focus, vertex, directrix, focal parameter, xintercepts, yintercepts of the entered parabola To graph a parabola, visit the parabola grapher (choose the Find the vertex of this parabola y=4x^28x12 Get the answers you need, now!Given a parabola whose equation is {eq}y=x^24x3 {/eq} Then we have that {eq}a=1, b=4, c=3 {/eq} To graph the parabola we first have to find its characteristic points

Consider The Parabola Y 2 4x A 4 4 And B 9 6 Be Two Fixed Points On The Parabola Let C Be A Moving Point On The Parabola

The Area Bounded By The Curves Y 2 4x And X 2 4y Is Sarthaks Econnect Largest Online Education Community

Answer (1 of 11) Graphical Solution ANSWER These curves have very practical uses but it takes time for them to become friends for you Note the crossing of the y axis and the 5 constant term in the equation in this form Completing the square gives you the coordinates of the vertex SolvinSolution Given the line 5x y = b et us find the slope of the line Step 1 Differentiate wrt 'x' Let us find the slope of parabola Step 2 Differentiate wrt 'x' Step 4 Substitute the values of a and x in the equation of parabola to get y Step 5 Substitute the values of a, x and yAnswer to Find the following parabola's focus and directrix y = 4x^2 By signing up, you'll get thousands of stepbystep solutions to your

What Is The Area Bounded Between The Curves Y 4x X 2 Y 5 2x Quora

Parabolas

Free Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience

What Is The Volume Of The Region Bounded By Y 4x X 2 And Y X 2 If Rotated About The Line X 4 Quora

The Area Bounded By The X Axis And The Curve Y 4x X 2 3 Is Youtube

Y 2x 2 And 2y 4x 4 Graph

What Is The Area Bounded By The Parabolas Y2 4x And Y2 12x 36 Math Questions

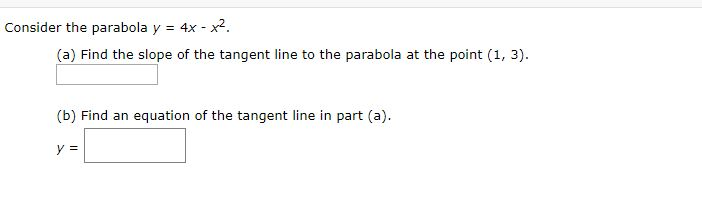
Consider The Parabola Y 4x X2 A Find The Slope Chegg Com

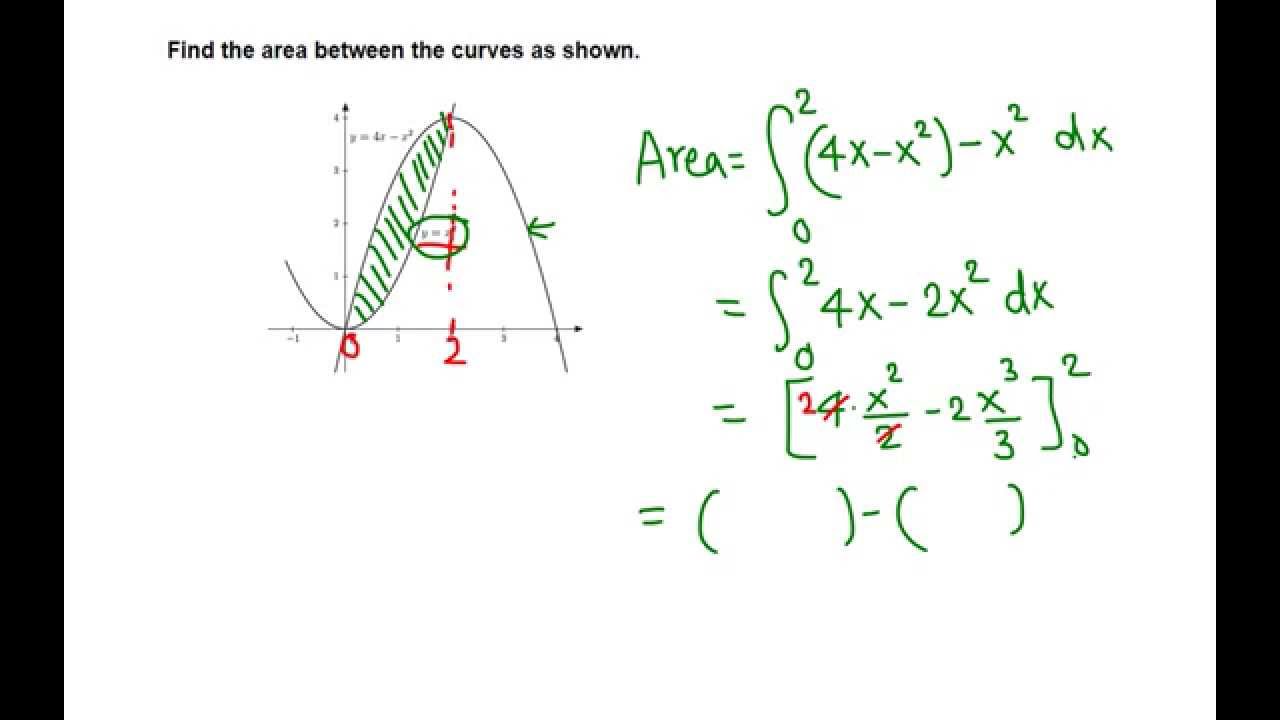
Area Between Y 4x X 2 And Y X 2 Youtube

Consider The Following Y X Y 4x X 2 About The Line X 5 A Set Up An Integral For The Volume Of The Solid Obtained By Rotating The

Find The Area Lying Above The X Axis And Under The Parabola Y 4x X 2

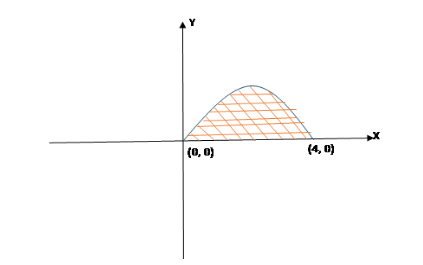
The Area Bounded By The Curve Y 4x X2 And The Xaxis Class 12 Maths Cbse

Solved Consider The Parabola Y 4x X 2 A Find The Chegg Com

Solution How Many Times Does The Parabola Y 4x 2 12x 9 Intersect The X Axis

Ex 21 1 Q4 Find The Area Lying Above The X Axis And Under The Parabola Y 4x X 2

Solution Graph The Parabola Y X2 4x 6

Where Do Y X 2 4x 1 And Y 3 X Intersect Mathskey Com

The Are Bounded By The Curve Y 4x X 2 And The X Axis Is

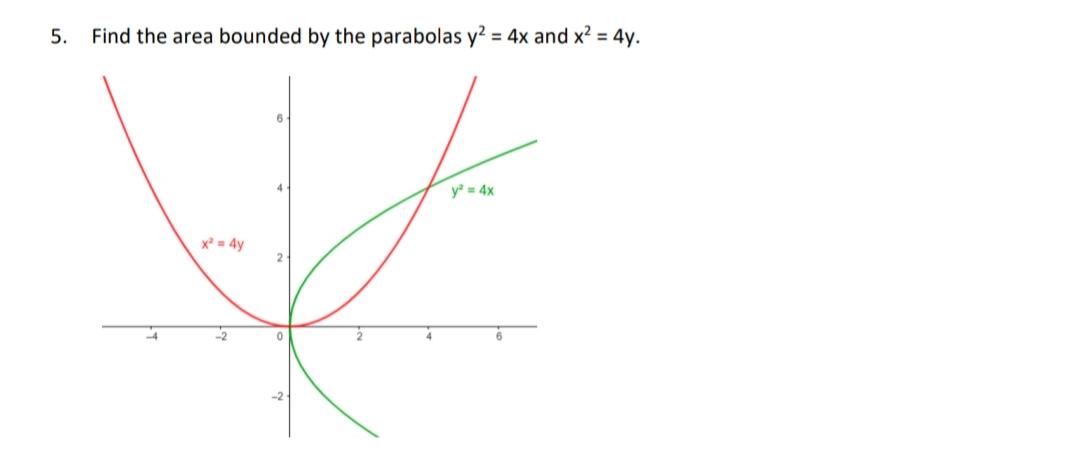
Solved 5 Find The Area Bounded By The Parabolas Y2 4x And Chegg Com

The Area Bounded By The Parabola Y 4x X 2 And X Axis Is

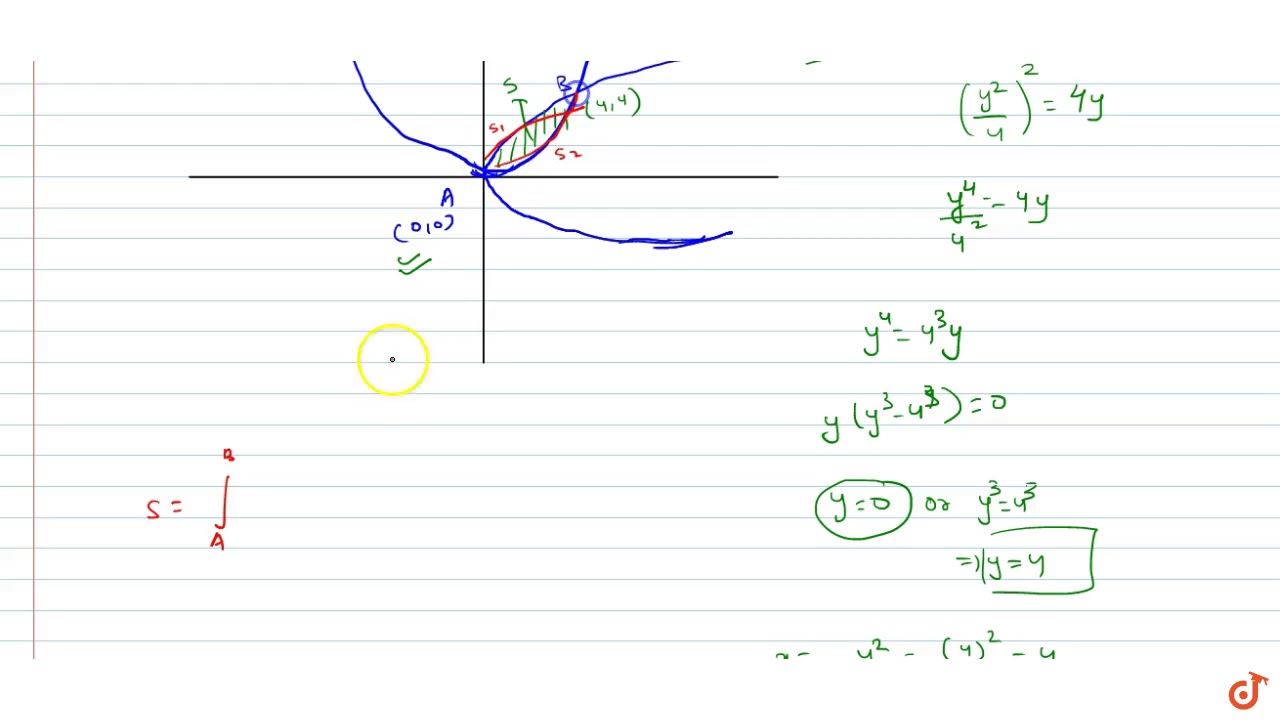
1

How Do You Find The Area Between The Curves Y 4x X 2 And Y X Socratic

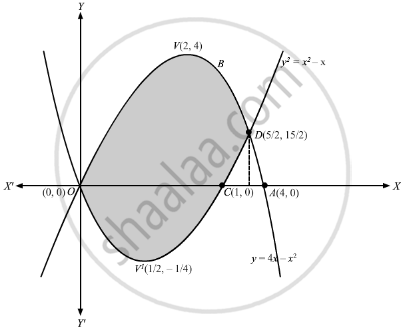
Find The Area Enclosed By The Parabolas Y 4x X2 And Y X2 X Mathematics Shaalaa Com

Solution Graph The Parabola Y X2 4x 4 Use The Quadratic Formula To Solve The Equation To The Exact Value Or Round To Two Decimal Places 2x 2 X 1

Grafica De La Parabola Y 4x X2 Donde X Es 2 1 0 1 2 3 4 Brainly Lat

Ex 8 1 11 Find Area Bounded By Y2 4x And Line X 3

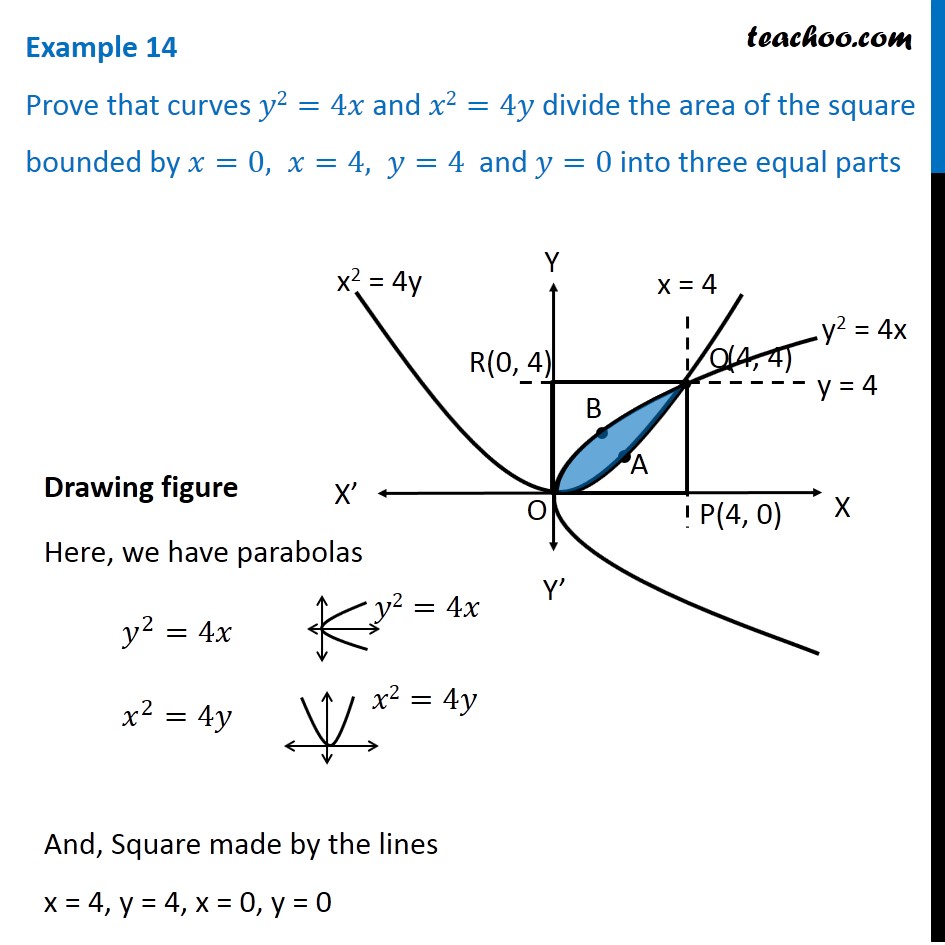
Example 14 Prove That Y2 4x X2 4y Divide Area Of Square

The Point Of Intersection Of The Tangents To The Parabola Y 2 4x At The Points Where The Circle X 3 2 Y 2 9 Meets The Parabola Other Than The Origin Is

Find The Area Of The Region Bounded By The Parabola Y 2 4x The X Axis And The Lines X 1 And X 4 Sarthaks Econnect Largest Online Education Community

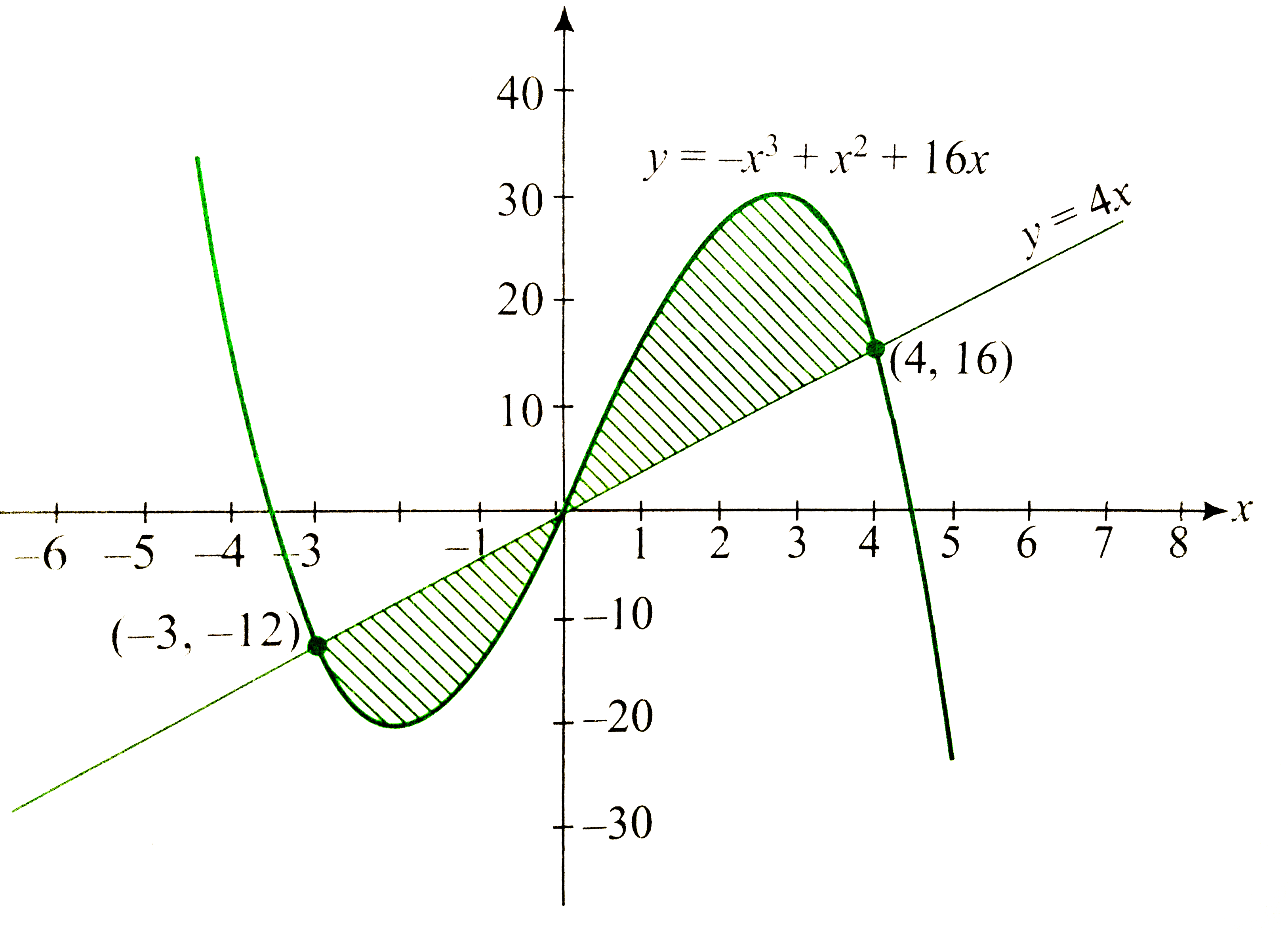
Find The Area Bounded By Y X 3 X 2 16x And Y 4x

Using Integration Find The Area Of The Region Bounded By The Two Parabolas Y 2 4x And X 2 4y Sarthaks Econnect Largest Online Education Community

Calcula El Area Del Recinto Limitado Por La Parabola Y 4x X 2 Y El Eje De Abscisas En El Brainly Lat

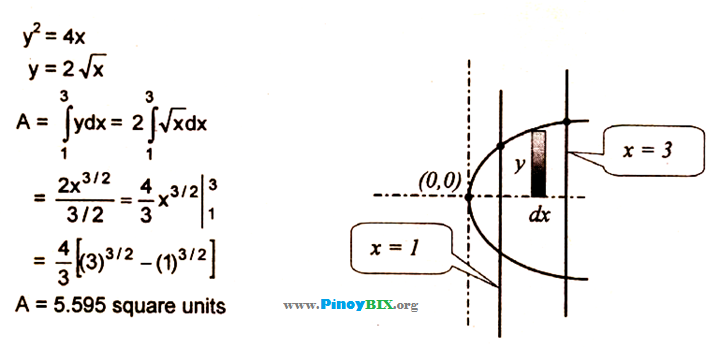
Solution Find The Area In The First Quadrant Bounded By The Parabola Y 2 4x

Exploration Of Parabolas

Hitunglah Luas Dataran Yang Dibatasi Oleh Parabola Y 4x X Dan Sumbu X Brainly Co Id

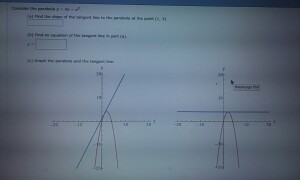
Consider The Parabola Y 4x X 2 Graph The Parabola And The Tangent Line To The Parabola At The Point 1 3 Study Com

The Area Bounded By The Parabola Y 4x 2 Y X 2 9 And The Line Y 2 Is A sqrt2 3 B 10sqrt2 3 C 40sqrt2 3 D Sqrt2 3

Let P Be The Point On The Parabola Y 2 4x Which Is At The Shortest Distance From The Center S Of The Circle X 2 Y 2 4x 16y

Find The Area Lying Above The X Axis And Under The Parabola Y 4x X 2 Sarthaks Econnect Largest Online Education Community

The Area Bounded By The X Axis And The Curve Y 4x X 2 3 Is

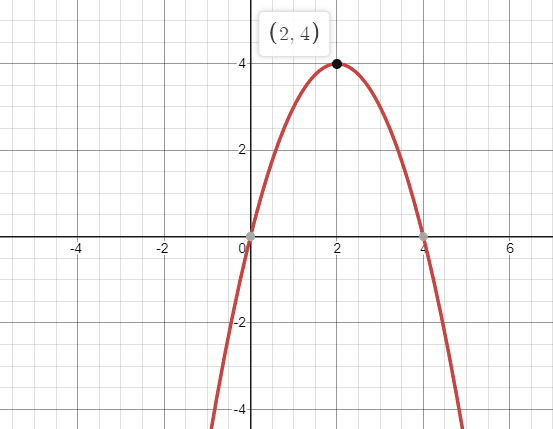
What Is The Vertex Of The Parabola Y 4x X2 Class 11 Maths Cbse

What Is The Volume Of The Solid Bounded By The Parabola Y 4x 2 And The Lines X 0 And Y 16 By Revolving About The Line Y 2 Quora

Example 14 Prove That Y2 4x X2 4y Divide Area Of Square

Y X2 Double Integral Of The Area Of The Y 4x X Region Homeworklib

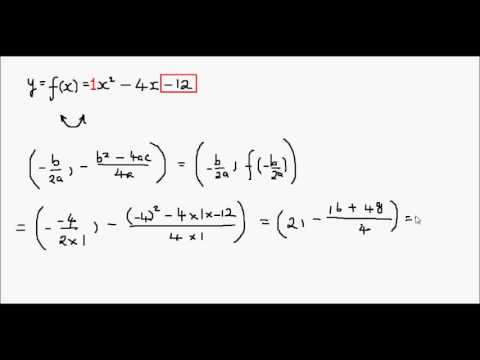
How To Sketch A Parabola Example 2 Y X 2 4x 12 Youtube

How To Graph A Parabola Y 4x 2 Socratic

Find The Area Of The Region Bounded By The Parabola Y 2 4x The X Axis And The Lines X 1 And Youtube

Solved Consider The Parabola Y 4x X2 A Find The Slope Chegg Com

In What Ratio Does The X Axis Divide The Area Of The Region Bounded By The Parabolas Y 4x X 2 And Y X 2 X Sarthaks Econnect Largest Online Education Community

Find The Area Lying Above The X Axis And Under The Parabola Y 4x X 2 Sarthaks Econnect Largest Online Education Community

Sketch The Region R That Lies Below The Parabola Y 4x X 2 Above The X Axis And Above The Line Y 3x 6 Find The Area Of This Region R Study Com

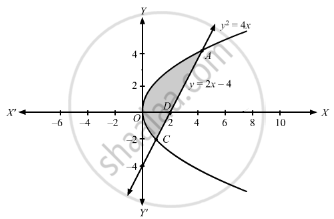
Find The Area Bounded By The Parabola Y2 4x And The Line Y 2x 4 I By Using Horizontal Strips Ii By Using Vertical Strips Mathematics Shaalaa Com

1

In What Ratio Does The X Axis Divide The Area Of The Region Bounded By The Parabolas Y 4x X2 And Y X2 X Mathematics Shaalaa Com

Solution What Is The Vertex Of The Parabola Y 4x 2 8x 3 What Is A Parabola

Find The Area Enclosed By The Parabolas Y 4x X 2 And Y X 2 X Sarthaks Econnect Largest Online Education Community

Solved Consider The Parabola Y 4x X2 Find The Slope M Chegg Com

Ex 8 2 7 Mcq Area Lying Between Y2 4x And Y 2x Is

Solved Consider The Parabola Y 4x X2 A Find The Slope Chegg Com

Find The Area Of The Region Bounded By The Curve Y2 2x And X2 Y2 4x Studyrankersonline

Q Find The Area Bounded By The Parabolas Y2 4x And X2 4y Brainly In

Find The Area Bounded By The Curve Y 4x X 2 The X Axis And The Ordinates X 1 And X 3

Find The Area Bounded By The Curve Y 4x X 2 The X Axis And The Ordinates X 1 And X 3 Youtube

1 Evaluate Definite Integral Cz Y Y2107 2 A Chegg Com

How To Write Y 4x X 2 As A Function With Respect To Y Mathematics Stack Exchange

The Region Between Y 4x X 2 And The X Axis Is Rotated Around The Y 6 Line How Can I Find The Volume Of The Object Formed Quora

Find The Area Of The Segment Cut Off From The Parabola Y 2 2x By The Line Y 4x 1 Sarthaks Econnect Largest Online Education Community

Solved 2 The Equation Of The Parabola Is Y X2 4x 3 Chegg Com

What Is The Area Bounded By X Axis And The Curve Math Y 4x X 2 Math Quora

Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube

Determine The Area Of The Region Bounded By The Parabola Y 4x 2 The Tangent Line To This Parabola At 2 16 And The X Axis Study Com

What Is The Area Of Region Enclosed By Parabola Y 2 X And Line Y X Quora

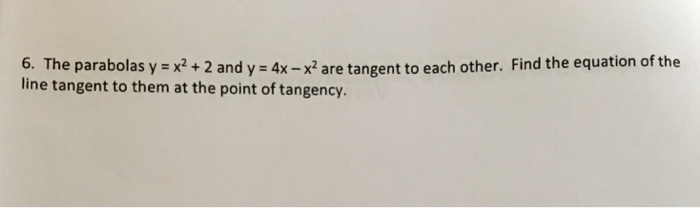
Solved The Parabolas Y X 2 2 And Y 4x X 2 Are Each Chegg Com

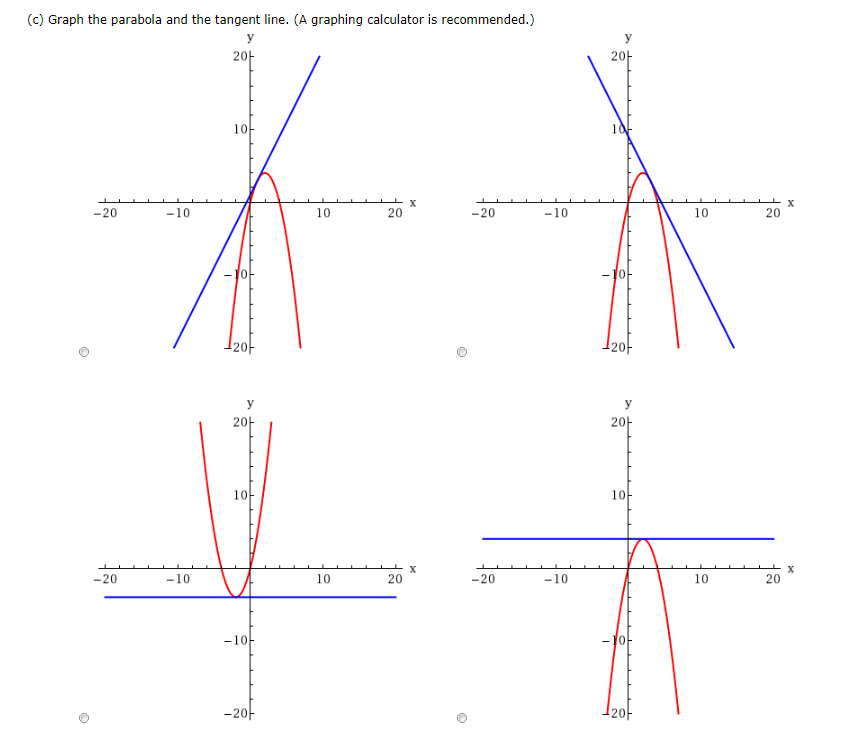
Solved Consider The Parabola Y 4x X2 A Find The Slope M Chegg Com

Consider The Parabola Y 4x X2 A Find The Slope O Gauthmath

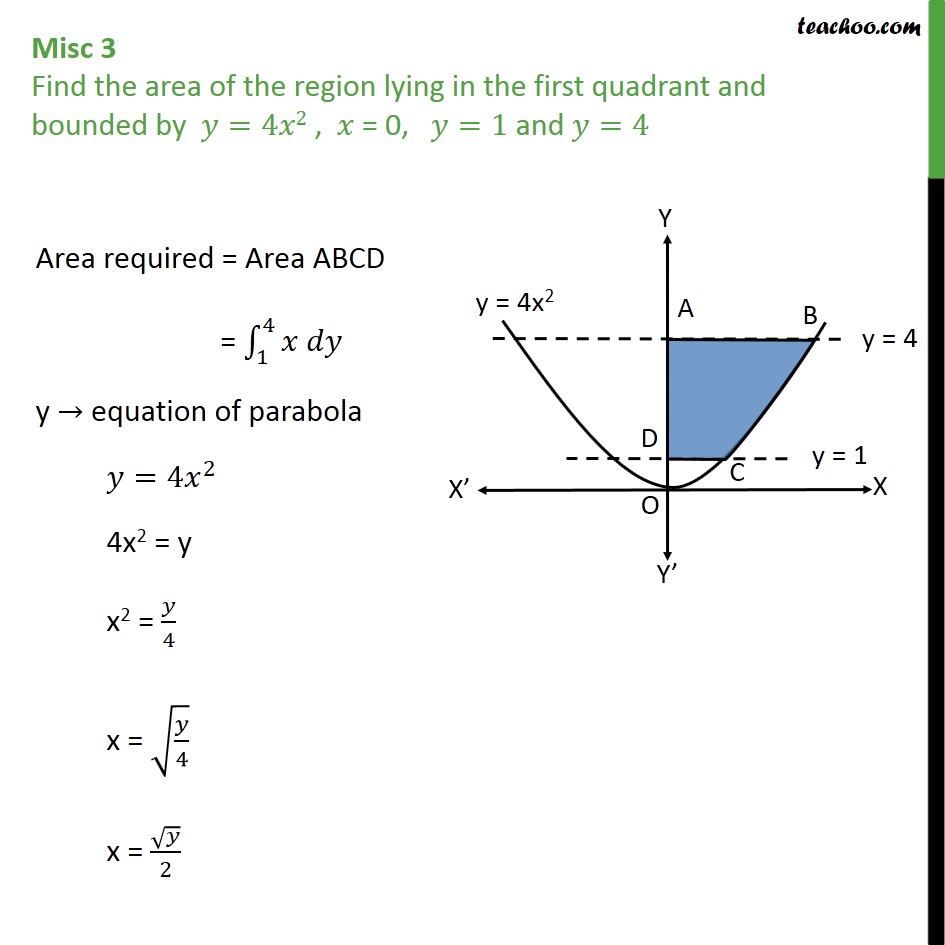
Misc 3 Find Area Bounded By Y 4x2 X 0 Y 1 Y 4

1

How Do You Graph Quadratic Functions Y X 2 4x 7 Socratic

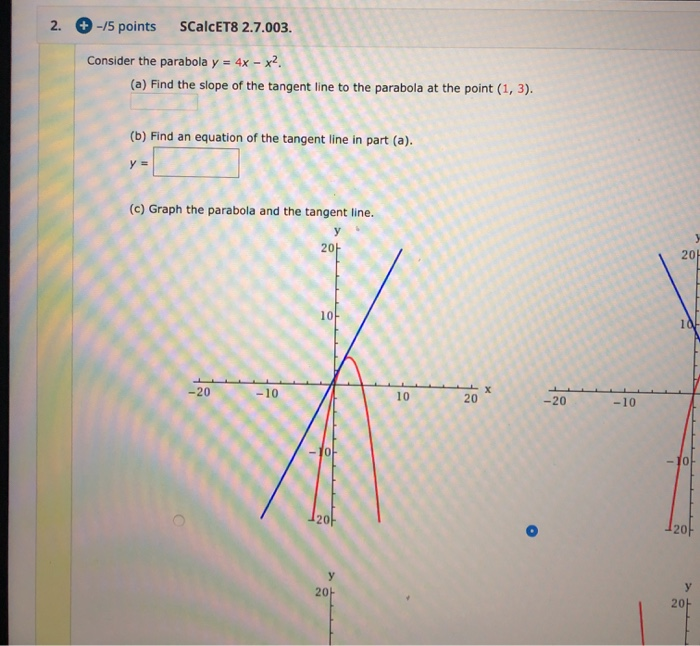
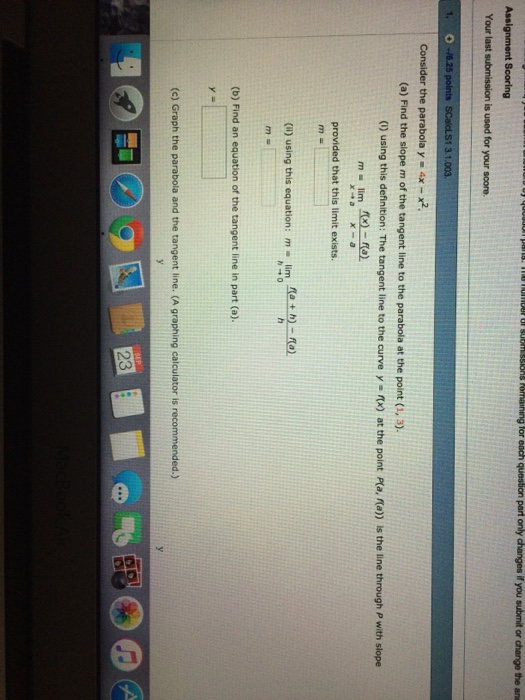
Solved Scalcet8 2 7 003 2 5 Points Consider The Parabola Chegg Com

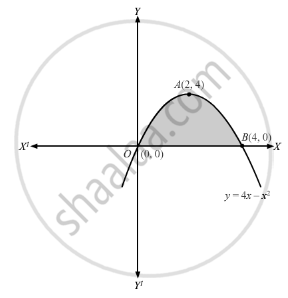
Find The Area Lying Above The X Axis And Under The Parabola Y 4x X2 Mathematics Shaalaa Com

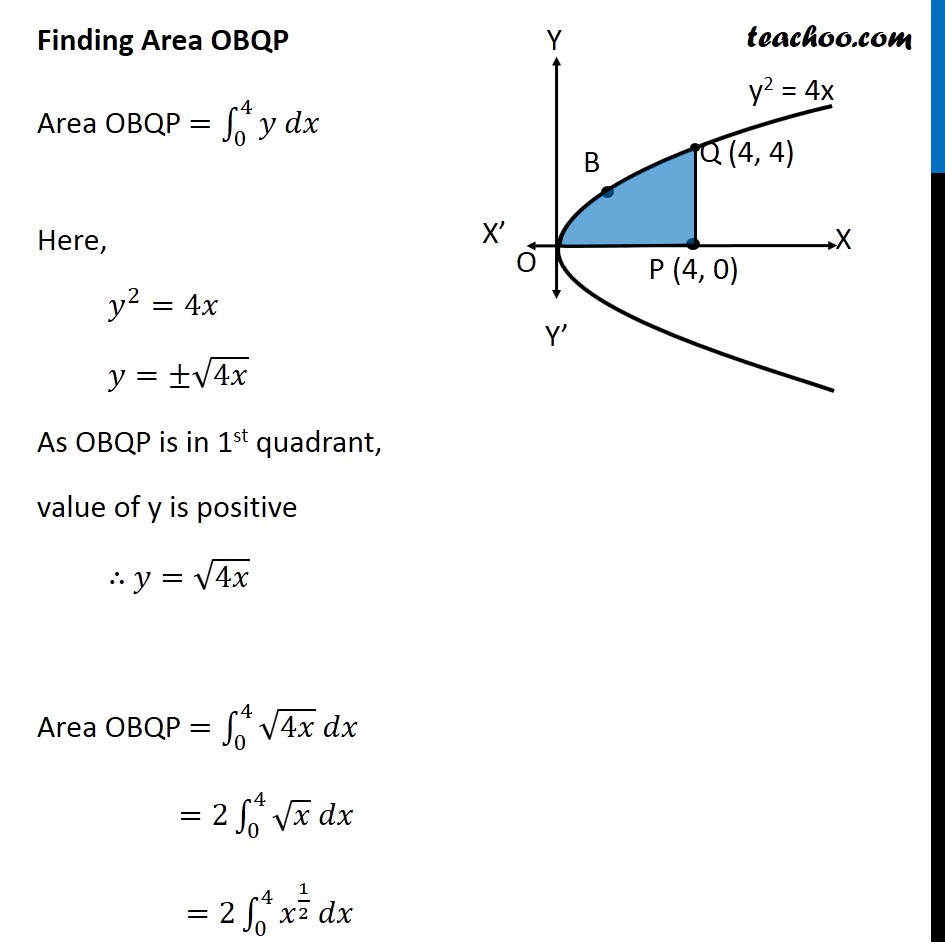
Example 14 Prove That Y2 4x X2 4y Divide Area Of Square

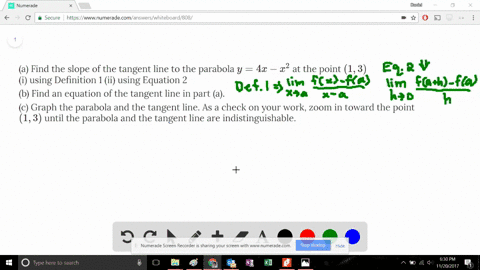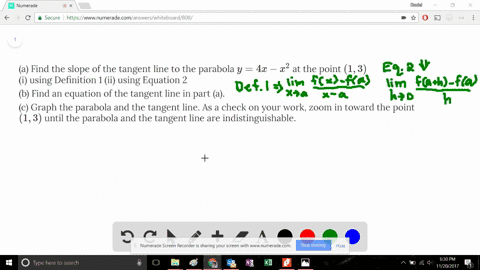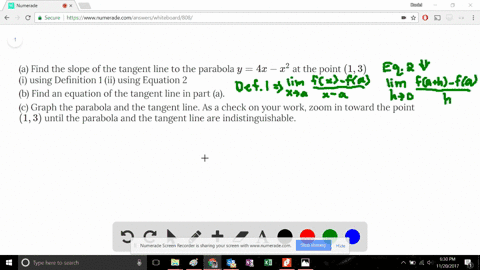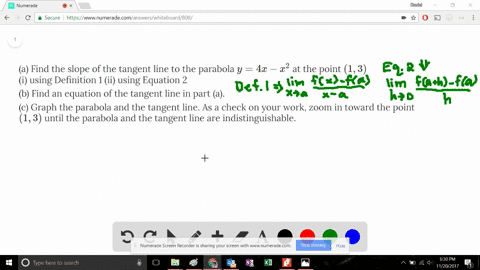
Solved A Find The Slope Of The Tangent Line To The Parabola Y 4x X 2 At The Point 1 3 I Using Definition 1 Ii Using Equation 2 B Find An

What Is The Vertex Of Y X 2 4x 1 Socratic