Y=x^2 2x-8 in vertex form 317809-Y=x^2+2x-8 in vertex form

This algebra 2 and precalculus video tutorial explains how to convert a quadratic equation from standard form to vertex form with and without using the complQuestion Write the function in vertex form y=x^23x6 Answer by Edwin McCravy You can put this solution on YOUR website!{eq}y = 2x^2 8x 11 {/eq} Graphing Quadratic Equations in Vertex Form In this solution, we are given a quadratic expression written as a sum of powers of {eq}x {/eq} and are tasked to write it

Ppt Converting Quadratic Equations Powerpoint Presentation Free Download Id

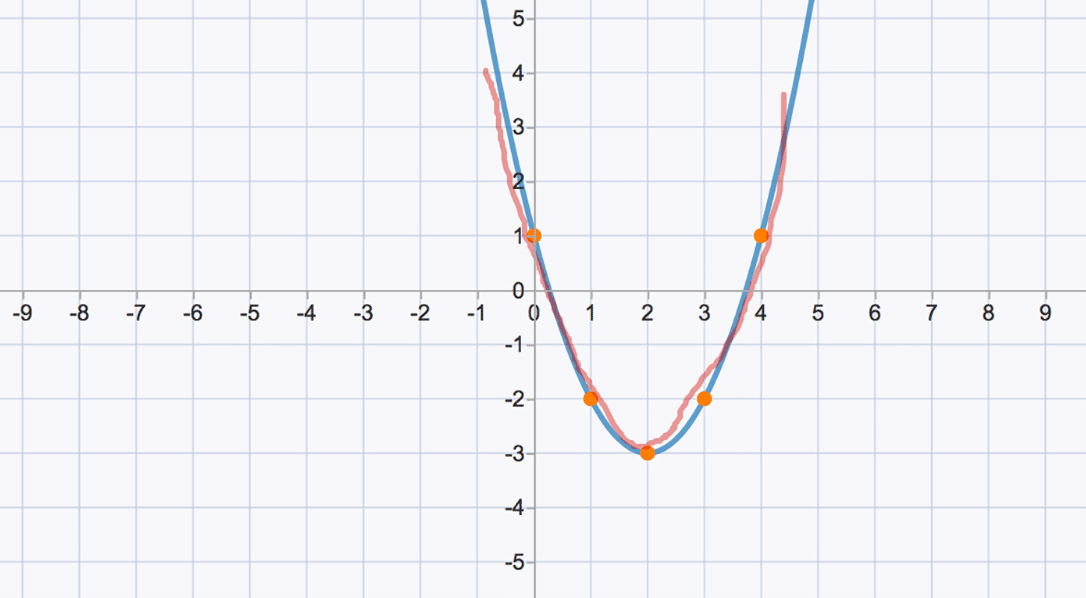
Y=x^2+2x-8 in vertex form

Y=x^2+2x-8 in vertex form-Of symmetry from Vertex Form Equation Problem 3 What is the following parabola's axis of symmetry of $$ y = (x 3)^2 4$$ What is the following parabola's axis of symmetry of $$ y =x^2 2x 3 $$ Answer Since this equation is in standard form, use the formula for standard form equation $$ x = \frac{ b}{ 2a} $$** y=x^(2)8x1 complete the square y=(x^28x16)116 y=(x4)^217 This is an equation of a parabola that opens upwards with vertex at (4,17) Its standard form of equationy= (xh)^2k, (h,k) =(x,y) coordinates of the vertex

Www Sanjuan Edu Site Handlers Filedownload Ashx Moduleinstanceid 598 Dataid Filename Unit 3 final review answers Pdf

 But the equation for a parabola can also be written in "vertex form" y = a(x ?Registered From Posted Saturday 30th of Dec 0933 Hi, I am a senior in high school and need major help in convert to vertex form calculator My math grades are awful and I have decided to do something about it I am looking for some software that will allow me to enter a question and gives detailed step by step solution The question is asking us to find which function in the vertex form is equivalent to f ( x ) = 4 x^2 2 x We have to add 1 to make a squared binomial ( and also to subtract 1 ) f ( x ) = ( x^2 2 x 1 ) 1 4 = ( x 1 )^2 3

Examples vertex\y=x^ {2}2x3 vertex\y=3x^ {2}5x vertex\y=x^ {2} vertex\y=2x^ {2}2x2 functionvertexcalculator vertex y=x^ {2}2x3 en36 is the value for 'c' that we found to make the right hand side a perfect square trinomial;Expand the expression in the

Y = a x 2 b x c But the equation for a parabola can also be written in "vertex form" In this equation, the vertex of the parabola is the point ( h, k) You can see how this relates to the standard equation by multiplying it out y = a ( x − h) ( x − h) k y = a x 2 − 2 a h x a h 2 k This means that in the standard form, y Find the vertex of the function y = –x2 2x 8 It is where the derivative 2x 2 = 0 Since you probably haven't learned about derivatives, do it this way Rewrite is as x^2 2x 8 = (x1)^2 7 Now look at the form of the formula on the right ItAlgebra Find the Vertex y=2x^24x8 y = 2x2 4x − 8 y = 2 x 2 4 x 8 Rewrite the equation in vertex form Tap for more steps Complete the square for 2 x 2 4 x − 8 2 x 2 4 x 8 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 2, b = 4, c = − 8 a = 2, b = 4, c

Quadratic Function Wikipedia

4 Convert Each Equation From The Vertex Form To T Gauthmath

To find the vertex form of the parabola, we use the concept completing the square method Vertex form of a quadratic function y = a(x h) 2 k In order to find the maximum or minimum value of quadratic function, we have to convert the given quadratic equation in the above form Minimum value of parabola31 Find the Vertex of y = x 22x48 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) We know this even before plotting "y" because the coefficient of the first term, 1 , Complete the square to rewrite the quadratic function in vertex form y = x ^ 2 2x 8 Answers 3 Get Other questions on the subject Mathematics Mathematics, 1530, southerntouch103 Gretchen is setting up

Q Tbn And9gcsl0jyluxfxjjcizs7jyiyflsxbm6hpbpzdawckl4kjhmo0pmir Usqp Cau

7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download

Adding 18 to both sides gives us a perfect square trinomial on the right; Explanation Vertex form is given by y = a(x − h)2 k with (h,k) being the vertex To get to vertex form, complete the square y = 2(x2 1 2x( 1 42) − ( 1 42)) − 1 y = 2(x 1 4)2 − 1 2 − 1 y = 2(x 1 4)2 − 11 8 and the vertex is ( − 1 4, − 11 8) Note If you want to just find the vertex using ax2 bx c h = − b 2aOur equation is in standard form to begin with y=ax 2 bxc;

Q Tbn And9gcrp9hpi7emwokn0e2fajh3aom0rmz7yizyhaftxq5127se4oc4j Usqp Cau

Finding Features Of Quadratic Functions Video Khan Academy

 #y = x^2 2x 8# #y 8 = x^2 2x 8 8# #y 8 = x^2 2x 8 8# #y 8 = x^2 2x# Now, the right side has the #ax^2 bx# terms, and we need to find #c#, using the formula #c = (b/2)^2# In our prepared equation, #b = 2#, so #c = (2/2)^2 = 1^2 = 1# Now, we add #c# to both sides of our equation, simplify the left side, and factor the right side Example 1 – The equation of a parabola is y=x^22x10 Write the equation in vertex form 1 Find a Looking at the equation, a = 1 2 Find vertex (h,k) The xcoordinate of the vertex is b/2a Looking at the equation, b = 2, and a = 1 as determined in the previous step1) write y=4x^232x66 in vertex form Complete the square y= 4x^32x64 66 64 y= (2x8)^2 2 vertex = 4,2 2)use the quadratic formula to solve the equation 4x^2x3=0

How To Put An Equation Into Vertex Form Quora

Transformations Of Quadratic Functions College Algebra

SOLUTION Write y=2x^212x14 in vertex form You can put this solution on YOUR website!Answer to Find the vertex formula, vertex, axis of symmetry, yintercept, xintercept, maximum and minimum Y=02x^22x8 By signing up, you'llAnswer to Convert y = 3x^2 12x 8 to vertex form By signing up, you'll get thousands of stepbystep solutions to your homework questions You

What Is The Axis Of Symmetry And Vertex For The Graph F X X 2 2x 8 Socratic

Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube

Example 13 Rewrite in y = a (x − h) 2 k form and determine the vertex y = 2 x 2 − 4 x 8 Solution Since a = 2, factor this out of the first two terms in order to complete the square Leave room inside the parentheses to add a constant term The equation is y = x 2 2x 2 To change the expression (x 2 2x) into a perfect square trinomial add (half the x coefficient)² to each side of the expression Here x coefficient = 2 So, (half the x coefficient) 2 = (2/2) 2 = 1 Add and subtract 1 to the expression y = (x 2 2x 2 1 1) y = (x 2 2x 1 2 1) y = (x 2 2x 1 3) y = (x 2 2(1)(x) 1 ²) 3Create your account View this answer The given equation is y =x2−2x−8 y = x 2 − 2 x − 8 To convert this into the vertex form, we have to complete the squares Adding 8 8 on both sides

5 Write The Equation Of The Parabola In Vertex Form Chegg Com

Fireworks From Standard To Vertex Form Ppt Video Online Download

All equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction 2x^ {2}6xy8=0 2 x 2 6 x − y − 8 = 0 This equation is in standard form ax^ {2Divide 22\sqrt {y} by 2 The equation is now solved Swap sides so that all variable terms are on the left hand side Factor x^ {2}2x1 In general, when x^ {2}bxc is a perfect square, it can always be factored as \left (x\frac {b} {2}\right)^ {2} Take the square root ofFind the Vertex Form y=x^22x8 y = x2 − 2x − 8 y = x 2 2 x 8 Complete the square for x2 −2x−8 x 2 2 x 8 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = − 2, c = − 8 a = 1, b = 2, c =

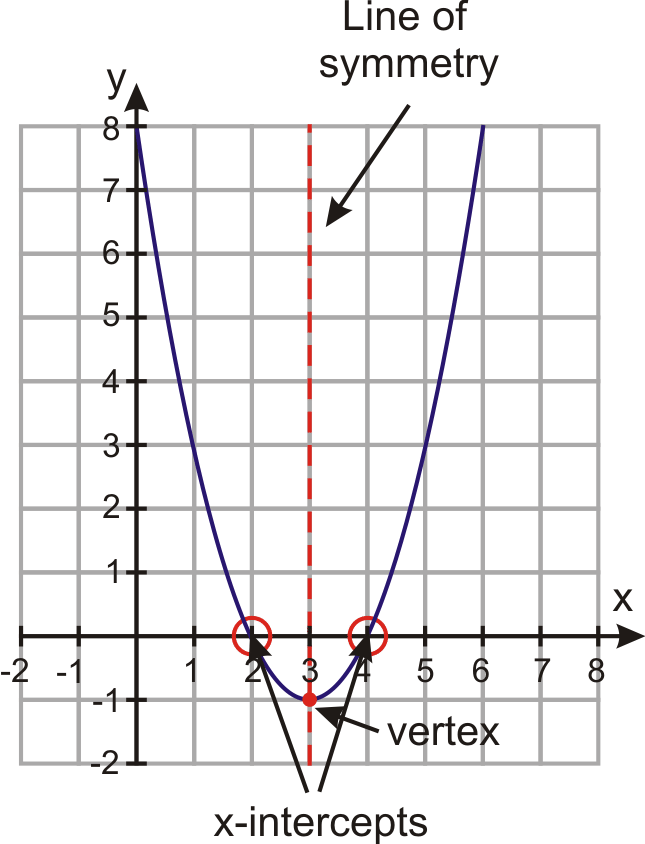
Mfg The Vertex Of A Parabola

Parabolas In Standard Intercept And Vertex Form Video Lesson Transcript Study Com

This video screencast was created with Doceri on an iPad Doceri is free in the iTunes app store Learn more at http//wwwdocericomWhat is y=x^(2)8x1 in vertex form?PARABOLAS IN VERTEX FORM To find vertex of a parabola convert it into vertex form y = a (x h ) 2 k Point (h, k) is the vertex of the parabola Example 1 Find the vertex of the parabola

How Do You Find The Vertex Of The Parabola Y 2x 2 8x 7 Socratic

Http Www Mrsfruge Com Uploads 1 2 0 0 P2a 3 3 Quadratic Functions Packet Pdf

 8 The equation of a parabola in vertex form is y = a(x 2)² 5 If the parabola passes through the point (4, 21), what is the value of a?While the standard quadratic form is a x 2 b x c = y, the vertex form of a quadratic equation is y = a ( x − h) 2 k In both forms, y is the y coordinate, x is the x coordinate, and a is the constant that tells you whether the parabola is facing up ( a) or down ( − a ) (I think about it as if the parabola was a bowl of applesauceFind the Vertex Form y=2x^28x3 y = −2x2 8x 3 y = 2 x 2 8 x 3 Complete the square for −2x2 8x3 2 x 2 8 x 3 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = − 2, b = 8, c = 3 a = 2, b = 8, c = 3 Consider the vertex form of a parabola

Graph The Quadratic Function Y X 2 2x 3 Vertex X Y Intercepts Symmetry Domain Range Youtube

2

The vertex of a quadratic equation in vertex form is (h,k), so our vertex is (3,22)We can convert to vertex form by completing the square on the right hand side;Factor out the leading coefficient This step is important since we want the coefficient to be 1 Add this number () to the expression inside the parenthesis Now the

Graphs Of Quadratic Functions In Intercept Form Read Algebra Ck 12 Foundation

Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21

We want to put it into vertex form y=a(xh) 2 k;Enter your answer in the box below A Categories Uncategorized Leave a Reply Cancel reply Your email address will not be published Required fields are marked * 👍 Correct answer to the question Use completing the square to rewrite the equation y = x^2 2x8 in vertex form Identify the vertex eeduanswerscom

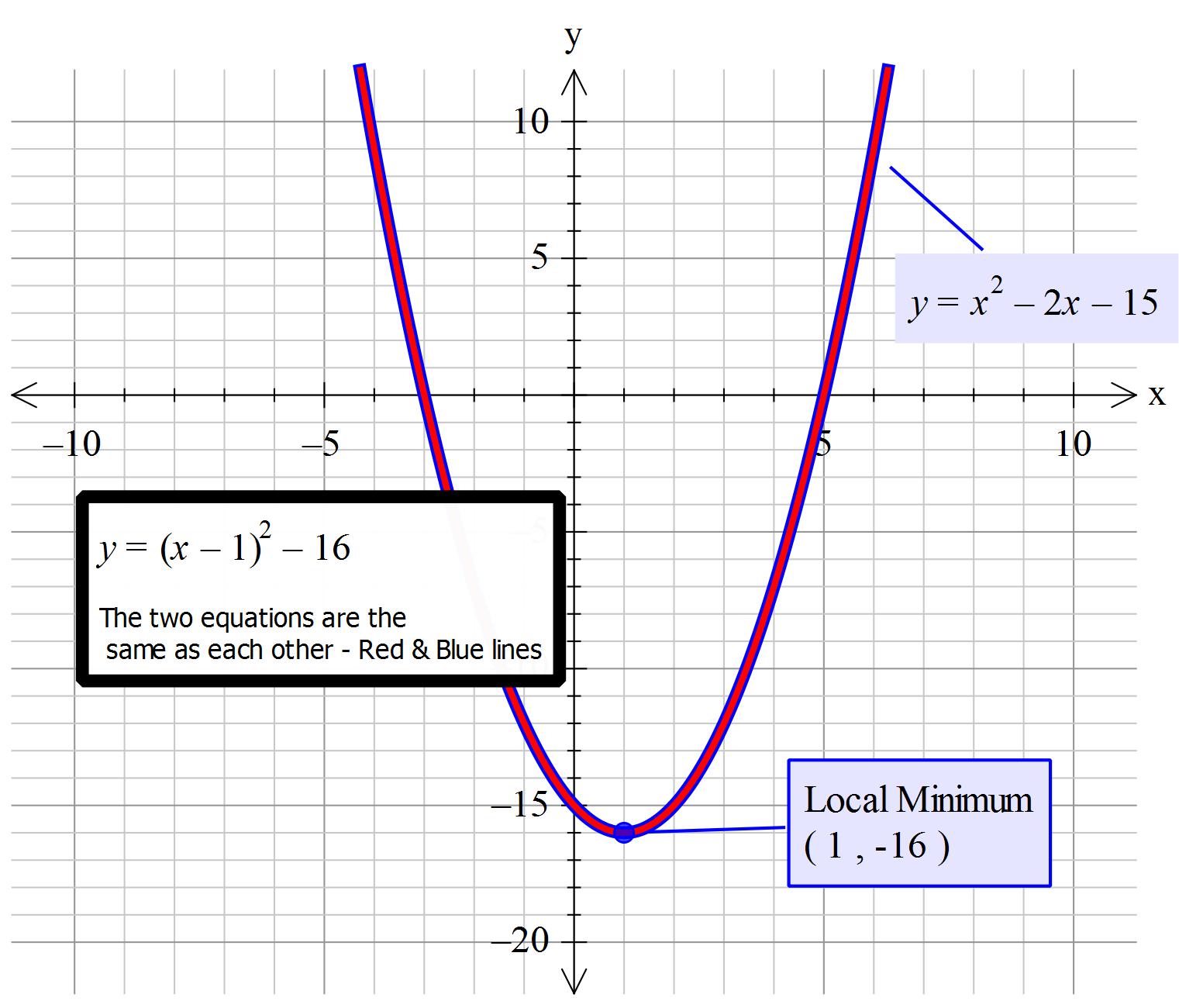
What Is The Vertex Form Of Y X 2 2x 15 Socratic

Write X 2 4x 3 In The Form Y X H 2 K Chegg Com

We want to put it into vertex form y=a(xh) 2 k;Find the Vertex y=2x^28 Rewrite the equation in vertex form Tap for more steps Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Simplify the right sideSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

Complete The Square Lesson Ppt Download

Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21

This algebra video tutorial explains how to convert a quadratic equation from standard form to vertex form and from vertex form to standard form This videoVertex Form y = a(xh)^2k where (h,k) is the vertex What is the vertex form of f(x)=x^22x5y5 = x^22xComplete the square on the xterms y5 1 = x^22x1Simplify the left and factor the right side to get y 6 = (x1)^2 y = (x1)^26Vertex at (1,6) ===== GraphStep 1 use the (known) coordinates of the vertex, ( h, k), to write the parabola 's equation in the form y = a ( x − h) 2 k the problem now only consists of having to find the value of the coefficient a Step 2 find the value of the coefficient a by substituting the coordinates of point P into the equation written in step 1 and solving

Vertex Axis Of Symmetry Of A Parabola Video Khan Academy

Fireworks From Standard To Vertex Form Ppt Video Online Download

Learn how to graph any quadratic function that is given in vertex form Here, Sal graphs y=2(x2)²5 Learn how to graph any quadratic function that is given in vertex form Here, Sal graphs y=2(x2)²5 If you're seeing this message, it means we'reWe can convert to vertex form by completing the square on the right hand side;The vertex form is a special form of a quadratic function From the vertex form, it is easily visible where the maximum or minimum point (the vertex) of the parabola is The number in brackets gives (trouble spot up to the sign!) the xcoordinate of the vertex, the number at the end of the form gives the ycoordinate

Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 p2 unit 2 2 note packet lg 1019 complete lt 8 to end Pdf

What Is Vertex Form Example Get Education

Complete the square to get the equation in vertex form with a = 16, h = 1, and k = 19 The path is a reflection over the xaxis and narrower It is also translated right 1 unit and up 19 unitsH)2 k Question Updated PM 1 Answer/Comment yeswey The minimum value of a parabola that opens upward will be its vertex TRUE Added PMIn comparing the graphs of y = x 2 (red), y = 2x 2 (green), and y = 4x 2 (blue), we see that each parabola opens upward but the larger the value of "a", the steeper (narrower) the graph Thus, when a ³ 1, the parabola opens upward, and as the value of

The Image Shows A Geometric Representation Of The Function F X X 2 2x 3 Written In Standard Brainly Com

Www Pittsfordschools Org Cms Lib Ny Centricity Domain 1335 homelearningquad1alg Pdf

Our perfect square trinomial factors into two identical binomials, (x6)•(x6) The vertex of an equation in vertex form Vertex form to standard form converter Our find the vertex calculator can also work the other way around by finding the standard form of a parabola In case you want to know how to do it by hand using the vertex form equation, this is the recipe Write the parabola equation in the vertex form y = a* (xh)² k;Select a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Replace the variable x x with 0 0 in the expression f ( 0) = ( 0) 2 − 2 ⋅ 0 − 8 f ( 0) = ( 0) 2 2 ⋅ 0 8 Simplify the result

3 Vertex Form

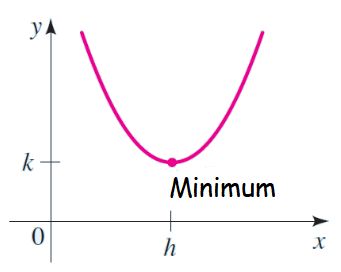
How To Find The Minimum Or Maximum Value Of A Function In Vertex Form

 y=(x1)^21 The equation of a parabola in color(blue)"vertex form" is color(red)(bar(ul(color(white)(2/2)color(black)(y=a(xh)^2k)color(white)(2/2)))) where (h ,k) are the coordinates of the vertex and a is a constant "Rearrange " y=x^22x" into this form" "using the method of "color(blue)"completing the square" y=(x^22xcolor(red)(1))color(red)(1) rArry=(x1)^21larrcolor(red)" in vertex form"We want to get y = a(xh)²k y = x²3x6 in the form Put brackets around the first two terms on the right, y = x²3x6 and since the coefficient of x² is 1 put 1 in front of the parentheses

Characteristics Of Quadratic Functions Math 1 Eoct Review

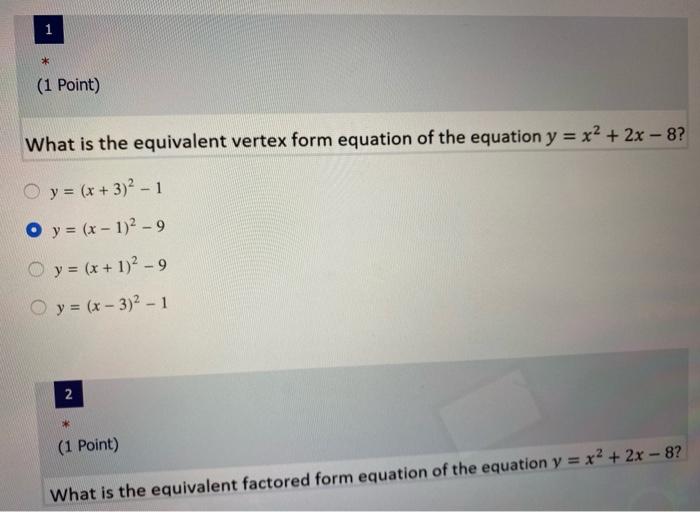
Solved 1 1 1 Point What Is The Equivalent Vertex For Chegg Com

Graphing Quadratic Functions

Www Scarsdaleschools K12 Ny Us Cms Lib Ny Centricity Domain 360 Convertvertexstandardform Pdf

Solved 1 1 1 Point What Is The Equivalent Vertex For Chegg Com

7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download

Http Www Manhassetschools Org Cms Lib8 Ny Centricity Domain 710 Group work 59 63 solutions Pdf

Ppt Converting Quadratic Equations Powerpoint Presentation Free Download Id

Converting A Quadratic Function From Standard Form To Vertex Form Completing The Square Youtube

Graphing Quadratic Functions

Www Sanjuan Edu Cms Lib Ca Centricity Domain 3740 Quadratics worksheet due monday sept25 Pdf

Quadratic Functions

Www Cravenk12 Org Cms Lib Nc Centricity Domain 1711 Unit 2 test quadratics review Pdf

The Vertex Form Of The Function Is Choose The Equation That Shows A Step In The Process Of Brainly Com

Question Video Identifying Vertex Form Of A Quadratic Expression Nagwa

2

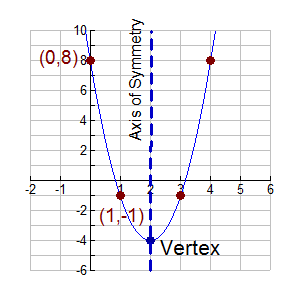
Vertex Form Of Quadratic Equation Mathbitsnotebook Ccss Math

Vertex Form Of A Quadratic Equation

Solution Write Each Function In Vertex Form Sketch The Graph Of The Function And Label Its Vertex 33 Y X2 4x 7 34 Y X2 4x 1 35 Y 3x2 18x 36 Y 1 2x2 5x

How To Graph Parabolas Krista King Math Online Math Tutor

How Do I Convert The Equation F X X 2 2x 3 To Vertex Form Socratic

Solution What Is The Vertex Form Of F X X 2 2x 5

Write The Equation In Vertex Form Y X 2 2x 8 Study Com

Vertex Intercept And Standard Form Ck 12 Foundation

Untitled Document

Y X

Rewriting Quadratics From Standard Form Into Vertex Form On Vimeo

Biomath Quadratic Functions

7 1 Graphs Of Quadratic Functions In Vertex Form Quadratic Flip Ebook Pages 1 39 Anyflip Anyflip

Vertex Form Of Parabolas Kuta Software

1

The Vertex Form Of The Equation Of A Parabola Is Y 1 2 X 4 Squared 13 What Is The Standard Form Of Brainly Com

Converting Quadratic Equations Worksheet Coach Forrester

No Pag D B Transform Each Vertex Form Of Quadrat Gauthmath

2 1 Graphing Quadratic Functions Quadratics Exploration Patty

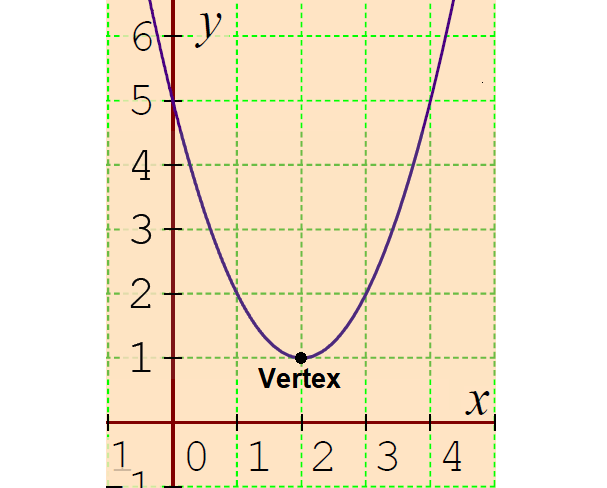
View Question What Is The Vertex Of The Equation Y X 2 2x 8

Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora

Www Sanjuan Edu Site Handlers Filedownload Ashx Moduleinstanceid 598 Dataid Filename Unit 3 final review answers Pdf

Find Factored Form And Vertex Of F X X 2 2x 8 Youtube

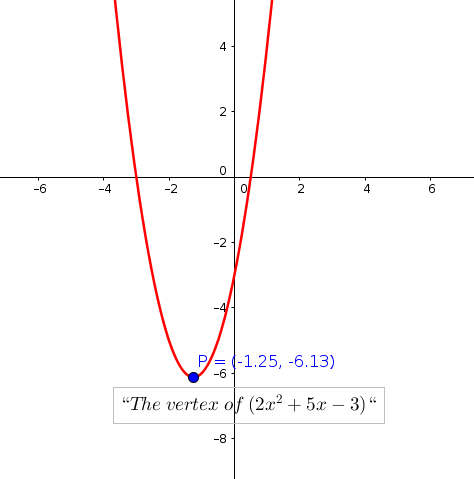
What Is The Vertex Form Of Y 2x 2 5x 3 Socratic

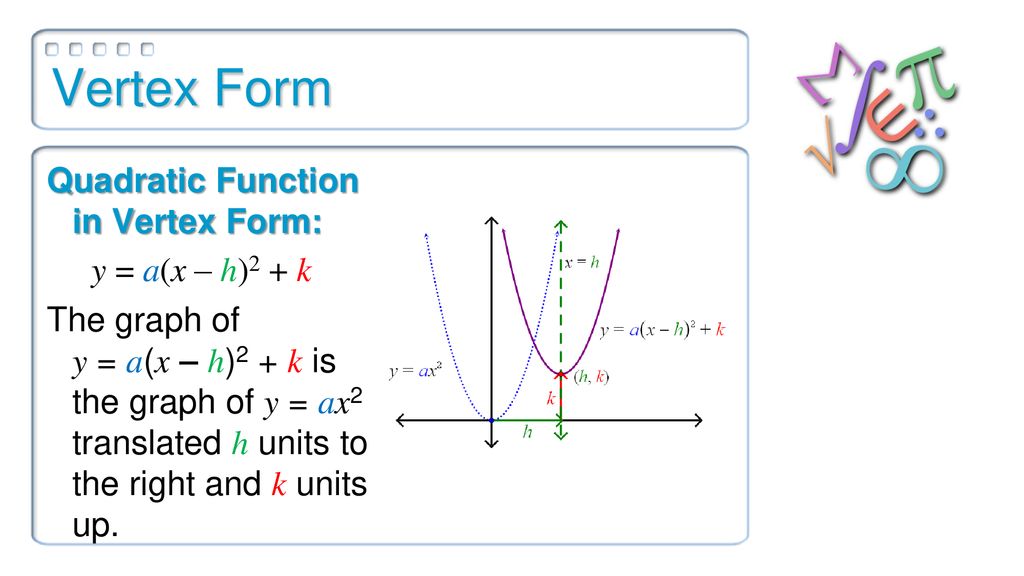
Vertex Form Quadratic Function In Vertex Form Ppt Download

Vertex Intercept And Standard Form Ck 12 Foundation

How To Put An Equation Into Vertex Form Quora

Solution Use The Graph Of Y X 2 2x 8 Does This Function Have A Maximum And Minimum And If So What Are They

Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21

Exercises 2 3 In Problems 1 8 Find The Vertex Form Of Chegg Com

Practice 1 2 Graphing In Vertex Form And Intercept Form

Quadratic Functions

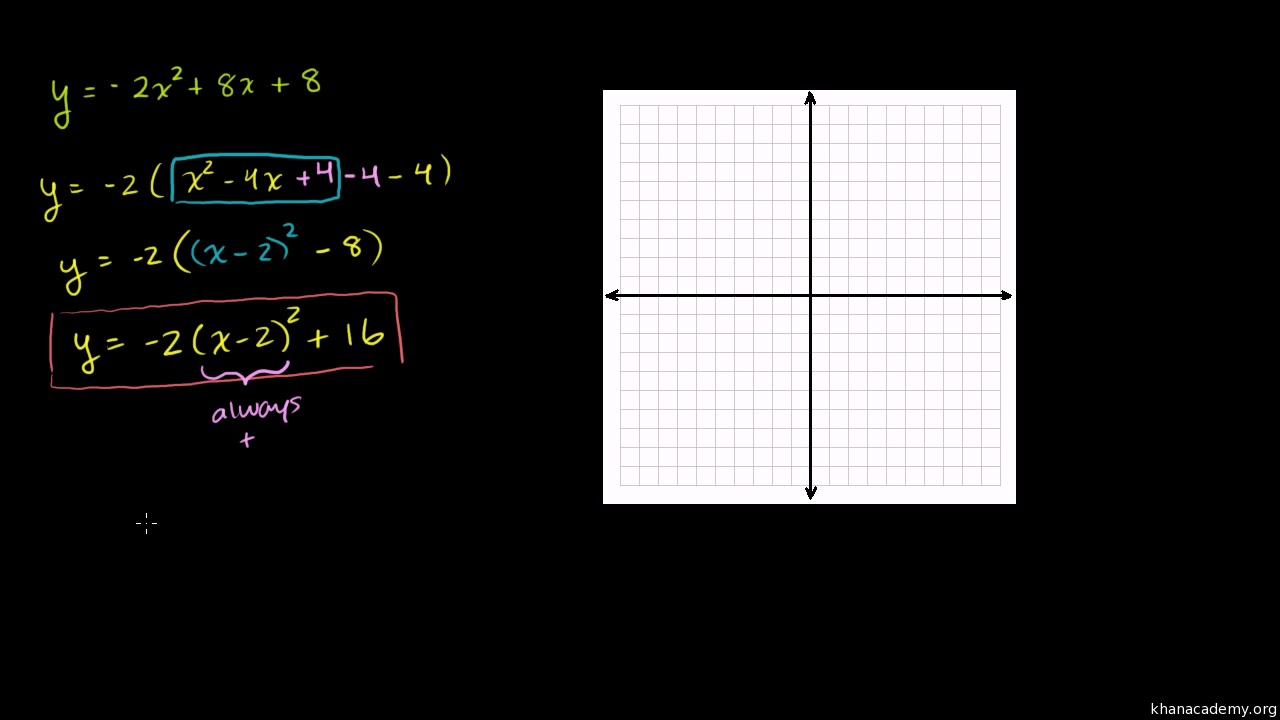
Vertex Axis Of Symmetry Of A Parabola Video Khan Academy

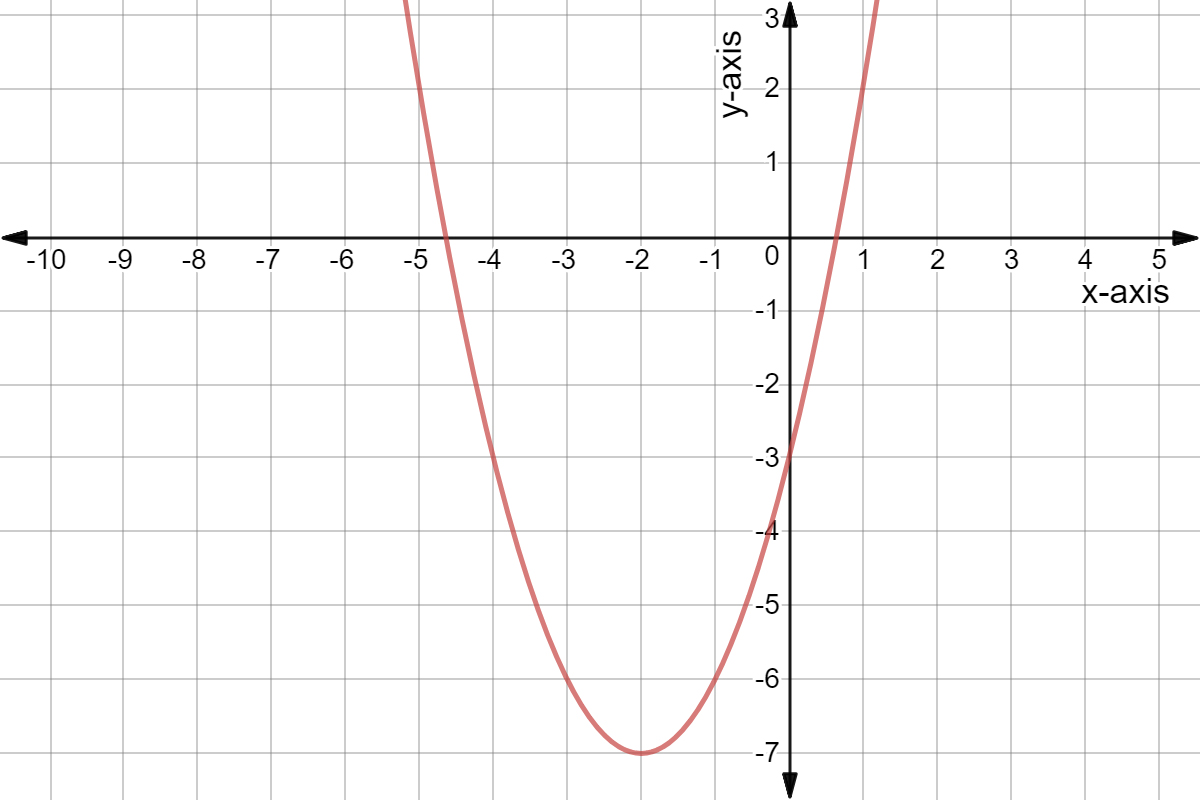
Completing The Square Vertex Form Of A Quadratic Expii

Vertex Form Of Quadratic Functions Math 2 Y

How To Graph A Quadratic Equation 10 Steps With Pictures

5 3 Vertex Form Of Quadratic Functions Translating Pages 1 4 Flip Pdf Download Fliphtml5

2

Standard Form To Vertex Form Definitions Facts And Solved Examples Cuemath

How To Graph A Quadratic Equation 10 Steps With Pictures

Vertex Form Vertex Form Vertex Form Is Another

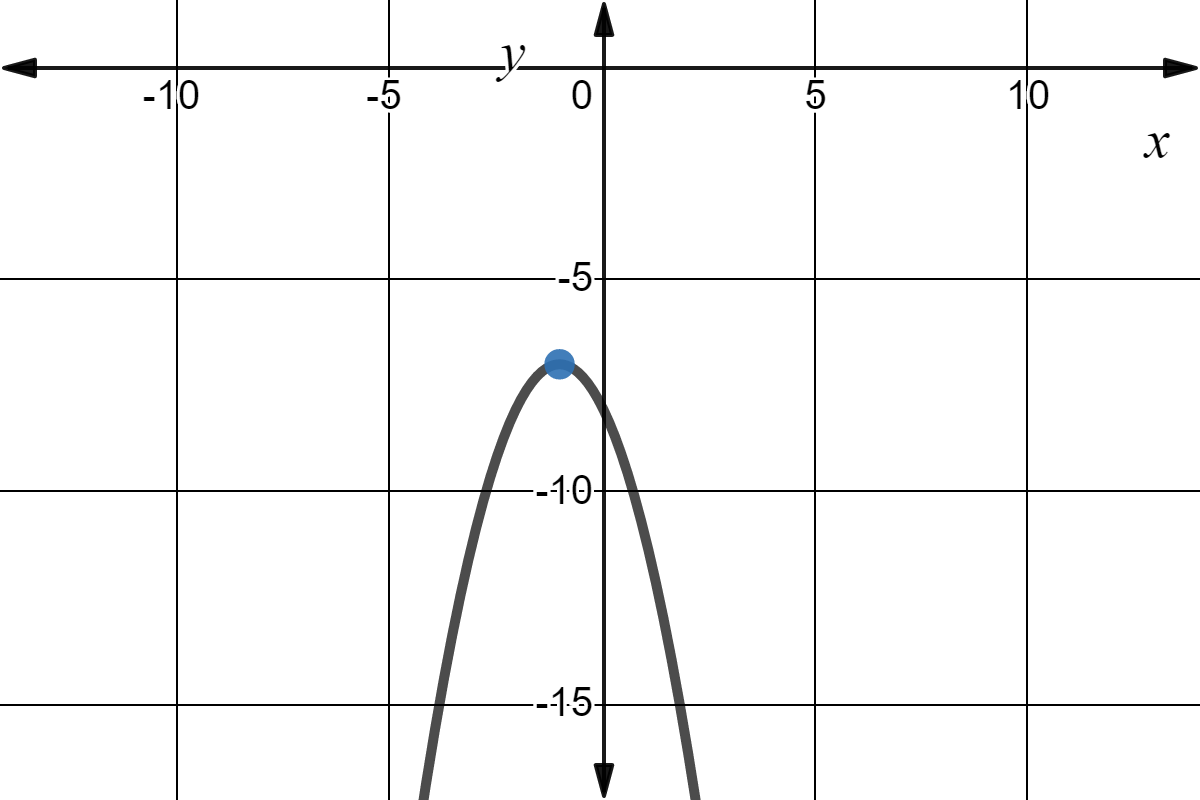
Intro To Quadratic Graphs Key Features Of Parabolas Expii

Vertex Form Request Y X 2 14x 11 Youtube

Y Classzone

1

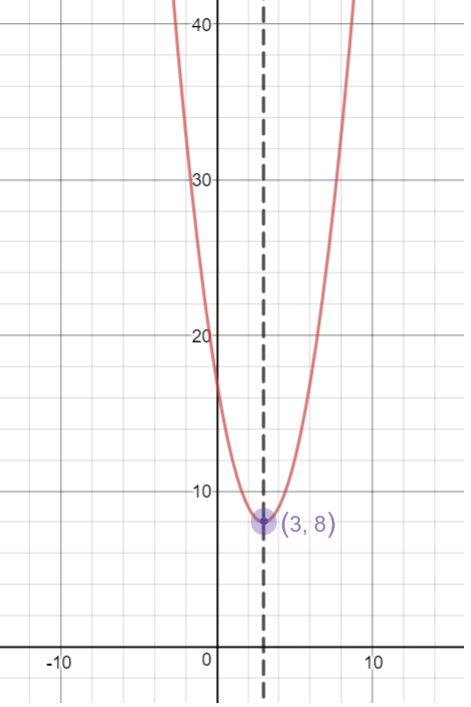
Vertex Form Of A Quadratic Equation Algebra Socratic

Example 4 Write A Quadratic Function In Vertex Form Write In Vertex Form Then Identify The Vertex X 2x 2 10x 22 Y Solution X 2x 2 10x 22 Y Write Ppt Download

Converting Quadratics Between Standard Factored And Vertex Form Qr Codes

Changing Quadratic Functions From Standard Form To Vertex Form Flashcards Quizlet

Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 a2 17 unit 2 2 ws packet lg Pdf

Biomath Quadratic Functions

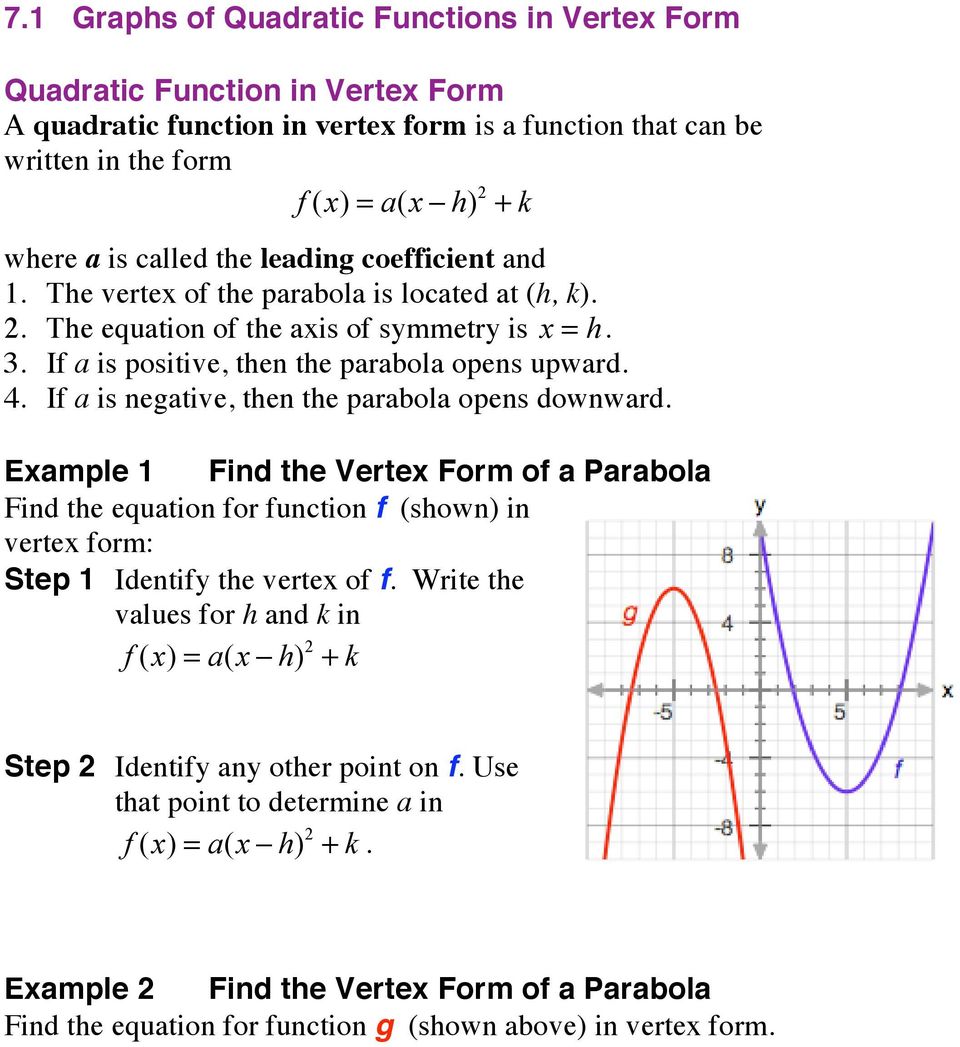
7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download

Http Www Midwayisd Org Cms Lib Tx Centricity Domain 164 Preap alg ii 4 7b Pdf

2

6 3 Interpreting Vertex Form And Standard Form Pdf

1 Find The Vertex Point H K 2 A Will Be The A From The Standard Form Equation 3 Substitute Into Y A X H 2 K Ppt Download

Incoming Term: y=x^2+2x-8 in vertex form,